3. INTERACTIONS AMONG PHASES

3.1. Evaporation and condensation

Thermal conduction tries to destroy multiphase structure by erasing temperature gradients. Whether this tendency toward homogenization leads to evaporation of clouds or the condensation of hot phase onto existing clouds depends on the cooling function in the hot phase, as well as the sizes and distribution of clouds. The efficiency of thermal conduction also depends on the magnetic connectivity between the phases, which is poorly understood. Although the conductivity perpendicular to a magnetic field line is almost completely suppressed, any connection between the phases, albeit by tangled field lines, is likely to suppress the conductivity only by a factor of a few (Tribble 1989). In a fully ionized cosmic plasma the "classical" coefficient of conductivity is

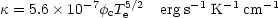
(7)

(Spitzer 1962; Draine and Giuliani 1984), where the factor _c 1 allows for a reduction in the mean free path due to magnetic fields or turbulence. Equation (7) is appropriate when the electron mean free path is sufficiently short compared to T / |T| that heat conduction can be treated in the diffusion approximation, 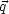= - T. When the diffusion approximation breaks down, the conductive heat flux first enters the saturated regime (Cowie and McKee 1977), q_sat = 5_s c_s p (where c_s = (p / )^1/2 is the isothermal sound speed in the intercloud medium and _s is a suppression factor similar to _c), and eventually the "suprathermal" regime (Balbus and McKee 1982), in which thermal conduction is best treated by a two-fluid approach.

The inhibition of multiphase structure by thermal conduction was first discussed by Field (1965), who found that conduction suppresses thermal instability for wavelengths shorter than a critical value which Begelman and McKee (1990) have generalized and dubbed the Field length,

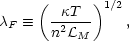
(8)

where _M Max(, / n). _F is the maximum length scale across which thermal conduction can dominate over radiative heating and cooling. Therefore, the thickness of a conductive interface with a radius of curvature r_c is ~ min(_F, r_c) (McKee and Cowie 1977). This implies that conduction into clouds with radii smaller than _F is unaffected by heating and cooling processes in the surrounding medium. Such "small" clouds always evaporate (Graham and Langer 1973; Cowie and McKee 1977), at a rate given by

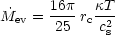
(9)

in the classical conduction limit. Clouds with radii larger than _F have conductive interfaces whose structures are independent of the cloud size; such interfaces are dominated by the balance between conduction and heating/cooling, and may be treated as plane-parallel.

Steady plane-parallel conduction fronts have been analyzed by Zel'dovich and Pikel'ner (1969), Penston and Brown (1970), and McKee and Begelman (1990). Ballet, Arnaud and Rothenflug (1986) and Böhringer and Hartquist (1987) studied non-equilibrium ionization in steady evaporative flows. Time-dependent mass exchange has been analyzed in one dimension by Doroshkevich and Zel'dovich (1981), by Balbus (1986b), who included magnetic fields, and by Borkowski, Balbus and Fristrom (1989) who also studied the ionization structure. If the hot phase is cooling (and is thermally unstable) then a cooling wave of fixed thickness propagates into the hot gas following an evaporative transient. Doroshkevich and Zel'dovich (and Böhringer and Fabian 1989) used this result to argue that steady-state evaporation solutions are incorrect, i.e., that all clouds embedded in a cooling background medium should condense, not evaporate. However, the evaporative transient lasts until the temperature gradient relaxes to the Field length, and the timescale for this to occur is the cooling time. The evaporative solutions found by Cowie and McKee (1977) persist over a time scale which is short compared to the cooling time, but long compared to the time required to set up the evaporation flow. If the hot phase is thermally stable, then there exists a "saturated vapor pressure" p_sat above which "large" clouds condense, and below which they evaporate (Penston and Brown 1970). Zel'dovich and Pikel'ner (1969) devised an approximate method for calculating the evaporation rate when p p_sat, which was refined and generalized to spherical clouds by McKee and Begelman (1990).