3.4. Dynamical considerations

Although there are models which obviate the need for relativistic bulk motion, it is important to emphasise that such motions are by no means unreasonable - and might even be expected. The brightness temperature limits tell us that the magnetic field is too weak to confine the relativistic plasma. So, unless this is bound by a much higher density of thermal plasma (and this can probably be excluded on other grounds), relativistic expansion would inevitably ensue. So these arguments, which are independent of the observed angular structure (and were even given prior to the VLB observations), at least support models involving intrinsic relativistic expansion.

The dynamics of a relativistic plasma have been discussed in a few idealized cases:

3.4.1. Free expansion of an initially uniform spherical cloud of relativistic gas [47]. If an initially uniform cloud of ultra-relativistic plasma starts expanding from radius r₀, then the Lorentz factor of the bulk expansion when the sphere has attained a radius r >> r₀, will be ~ r / r₀, the material then being mostly in a thin shell whose thickness remains ~ r₀. The internal energy per particle, measured in a comoving frame, would of course decrease by the same factor ~ r / r₀.

3.4.2. Steady relativistic wind Bernoulli's equation for a spherically symmetric relativistic outflow requires that the Lorentz factor for the bulk flow be proportional to r. Thus each comoving shell in the wind behaves rather like the expanding sphere in (i). Note that, if such a wind were to make a transition from subsonic to supersonic flow on passage through a "sonic radius" where the gravitational field plays the role of the nozzle (by analogy with the solar wind) then this would need to occur at a place where the escape velocity were c / 3 - i.e., near the Schwarzschild radius of a relativistically deep potential well [47].

3.4.3. Relativistic blast waves If a "point explosion" causes relativistic expansion of a blast wave into a uniform surrounding medium, then _blast r^-3/2. The swept-up particles acquire random energy, measured in a frame moving with the shock, corresponding to _blast. These particles are concentrated in a shell of thickness ~ ct _blast^-2 ( r⁴). When r gets so large that the shock stops being relativistic, there is a transition towards the ordinary Sedov solution. One can consider more general cases when the blast wave moves into a medium of non-uniform density or into a wind which itself has a relativistic outward velocity. This problem has been discussed in detail by Blandford and McKee [48].

Any of the above could be elaborated into a possible model or variable radio sources. Note, however, that one of the few things VLBI studies tell us unambiguously is that actual compact sources are not spherically symmetrical! Note also that the bulk expansion rate in models (i) and (ii) would in fact "saturate" at a finite equal to the mean initial Lorentz factor of the thermal motions of the ions. (If the plasma consists of electron-position pairs, the terminal could be much higher.) These models are applicable only if the external medium is rarified enough to be ignore. For a relativistic outburst of initial total energy , expanding with Lorentz factor , this requires

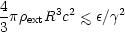
(12)

i.e., the particle density in the external medium must satisfy

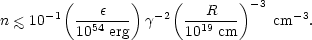
(13)

Otherwise the relativistic ejecta would be braked at too small a radius to account adequately for the radio structure.