1.2. Large-Scale Structure

The standard paradigm is that large-scale structures in the Universe are formed by gravitational instabilities, building on the primordial density perturbations observed in the CMB ⁽¹⁾, with baryons falling into the `holes' that are amplified by cold dark matter. Galaxy formation is considered to be more complex than cluster formation, with nonlinear astrophysical processes coming into play. Calculating galaxy formation is therefore more challenging numerically, though it may be guided by semi-analytical models. The general belief is that clusters formed before galaxies, which were formed by mergers of smaller structures.

The observational data on clusters of galaxies support the `concordance model' in several different ways. Data on X-rays from rich clusters can be used to estimate the ratio <sub>m</sub> / <sub>b</sub> [10], the results suggesting again that <sub>m</sub> << 1. The evolution of large-scale structure as a function of redshift also supports the concordance model, there being many more clusters at high z than would be expected in an Einstein-de-Sitter cosmology with <sub>m</sub> ~ <sub>tot</sub> ~ 1 [11]. Moreover, the shape of the two-point correlation function for galaxy clusters, as measured by the REFLEX collaboration, agrees with the concordance model, and is very similar in shape to that of the two-point correlation function for galaxies. The overall normalization of the cluster correlation function is considerably higher, as expected from the `biasing' phenomenon, according to which rarer peaks are correlated more strongly than those of lower significance [11].

Several large new surveys of galaxy redshifts are underway, with some initial results from samples of ~ 10⁵ galaxies now becoming available. Results from the first release of Sloane Digital Sky Survey (SDSS) data (29,000 redshifts) agree very well with those from the 2dF (200,000 redshifts) team and from the LCRS data (26,000 redshifts). Once again, the shape of the two-point correlation function agrees very well with the concordance model, and disagrees with the Einstein-de-Sitter model.

Just as the CMB is expected to display several acoustic peaks, so also the galaxy correlation function is expected to exhibit baryonic `wiggles' on scales up to ~ 100 Mpc. There was recently a claim [12] to have observed an indication of them, but the amplitude was unexpectedly large, and a more recent reanalysis casts doubt on the `wiggle' interpretation [13], as seen in Fig. 3.

Figure 3. A recent reanalysis [13] of the data of [12] does not reveal any baryonic `wiggles'.

Models of structure formation are also constrained by data on quasars and Lyman forests. The numbers of high-z quasars are problematic for hot- and warm-dark-matter models, but are consistent with the concordance model. The data on Lyman forests are particularly interesting, because reduced nonlinearities render their interpretation less ambiguous than those of galaxies.

As repeatedly mentioned, all these data are consistent with the concordance model. Combining them with the CMB and high-z supernova data, one obtains the refined estimates:

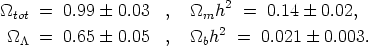
(2)

However, there are some open issues in structure formation. One is that walls of galaxies are seen in the data that do not appear in simulations, although this is not seen as a serious problem. Another potential problem is provided by density profiles in groups and clusters of galaxies, but here recent simulations now indicate that energy ejection due to supernovae breaks self-similarity in a manner consistent with observation, within the concordance model. There have also been worries about the numbers of satellite galaxies, with many fewer being observed than are expected in the concordance model. However, there are reasons to think that small galaxies might not light up [14], since their conventional matter could be dispersed by the radiation from the first generation of stars.

¹ Which are commonly thought to arise from an early epoch of inflation [8, 9]. Back.