2.2. Supersymmetric Dark Matter

Assuming that R (- 1)^{B + L + 2S} is conserved, the lightest supersymmetric particle (LSP) is stable, and may be an ideal candidate for cold dark matter, provided it is neutral and has no strong interactions. The possibility most often studied [49] is that the LSP is the lightest neutralino , a mixture of the supersymmetric partners of the photon, Z⁰ boson and neutral Higgs bosons. Another option mentioned here is that the LSP is the axino 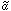, the supersymmetric partner of the hypothetical axion. Finally, there is the gravitino 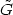, which is generally unwelcome, since detecting it would be very difficult. The gravitino option was not discussed here, so I do not discuss it either. Instead, I focus mainly on the lightest neutralino , mentioning more briefly the axino option.

Neutralino Dark Matter In some sense, the neutralino is the most `natural' candidate in the minimal supersymmetric extension of the Standard Model (MSSM), since one normally expects it to be lighter than the the gravitino in models based on supergravity, and a relic density in the range of interest to astrophysicists and cosmologists: 0.1 < h<sup>2</sup> < 0.3 is `generic'. As several speakers have shown here, neutralino dark matter is compatible with all the available accelerator constraints, including searches for supersymmetric particles at LEP [50], HERA [51] and the Tevatron collider, as well as the indirect constraints imposed by measurements of b s and g_µ - 2 [52, 53, 54, 55, 56]. In the most constrained versions of the MSSM, in which scalar and fermionic sparticle masses are each universal at some input grand-unification scale, as in simple supergravity (SUGRA) models, the lightest neutralino probably weighs more than about 100 GeV [57]. Figs. 10 and 11 show examples of the allowed parameter space in the constrained MSSM, illustrating the range allowed by the g_µ - 2 constraint at the 1.5- level, and the potential power of the search for B_s µ⁺µ^- at the Tevatron collider, respectively.

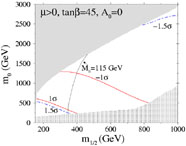
Figure 10. Compilation of limits on the constrained MSSM for µ > 0, tan = 45, A0 = 0, showing in particular the region favoured by gµ - 2 [54] at the ±1, 1.5- levels. Electroweak symmetry breaking is not posible in the shaded region at the top, and the lightest supersymmetric particle would be the lighter in the hatched region at the bottom.

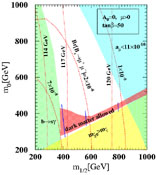
Figure 11. Compilation of limits on the constrained MSSM for µ > 0, tan = 55, A0 = 0, showing in particular the region accessible to the search for Bs µ+µ- at the Tevatron collider [55]. Regions on the left and right are disfavoured by b s and gµ - 2, respectively. In the hatched region at the bottom, the lightest supersymmetric particle would be the lighter . The allowed region for supersymmetric dark matter is shaded.

The allowed parameter space may be explored theoretically either by parameter scans, or by focusing on specific benchmark scenarios intended to illustrate the range of possibilities left open by the experimental constraints [58]. These indicate that dark matter searches can expect strong competition from future accelerators, notably the LHC. This will be able to explore much of the domain of parameters allowed by the relic density constraint and current experimental constraints. Moreover, as has been revealed by specific benchmark studies illustrtaed in Fig. 12, in much of the accessible parameter space the LHC may be able to discover several different types of supersymmetric particles, and measure the CMSSM parameters quite accurately. However, as also shown in Fig. 12, there are some benchmark scenarios where the LHC does little more than discover the lightest MSSM Higgs boson. Experiments searching for dark matter have an almost clear field until 2007, but will then get some serious competition: caveat the LHC!

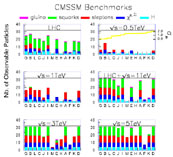
Figure 12. Summary of the prospective sensitivities of the LHC and lepton colliders with different s energies to CMSSM particle production in the proposed benchmark scenarios [58], which are ordered by their distance from the central value of gµ - 2, as indicated by the pale (yellow) line in the second panel. We see clearly the complementarity between a lepton ollider and the LHC in the TeV range of energies [58], with the former excelling for non-strongly-interacting particles, and the LHC for strongly-interacting sparticles.

Neutralino Relic Density Calculations These often assume universal input scalar masses, termed here the CMSSM, as found in minimal supergravity (mSUGRA) models. In the CMSSM, there is a `bulk' region of relatively low values of m<sub>1/2</sub>, m<sub>0</sub> where the relic density falls with in the range 0.1 < h<sup>2</sup> < 0.3 favoured by astrophysics and cosmology. Stretching out from the bulk region to larger m<sub>1/2</sub> and/or m<sub>0</sub> are filaments of parameter space where special circumstances suppress the relic density, in some of which the LSP mass m may be significantly heavier. These filaments may appear because of coannihilation [59] - in which the relic LSP density is suppressed by mutual annihilations with other sparticles that happen to be only slightly heavier, rapid annihilation through direct-channel boson resonances - in particular the heavier neutral MSSM Higgs bosons A, H, and in the `focus-point' region [60] near the boundary where calculations of electroweak symmetry breaking fail.

The relic density in the bulk region is relatively insensitive to the exact values of the input CMSSM parameters, and to differences in the (inevitable) approximations made in the calculations [61]. However, relic-density calculations in the filament regions are much more sensitive to these input values and approximations, and hence more likely to differ from one paper to another, as we have seen at this meeting. Several different codes for calculating the relic density are now available, and the most recent ones generally agree quite well, once the differences in inputs and approximations are straightened out.

Strategies to Search for Neutralinos The most direct signal for supersymmetric dark matter would be scattering on nuclei [62], a topic discussed by many speakers at this meeting. The observation of an annual modulation effect in the DAMA detector was reported here [63], but the source of the modulation has not yet been pinned down. Detectors using other techniques have not yet been able to confirm the DAMA results [64], but neither have they yet been ruled out. Most calculations now agree that it is very difficult to reproduce in the constrained MSSM the elastic scattering cross section that would be required by DAMA [52, 56, 65], as seen for example in Fig. 13.

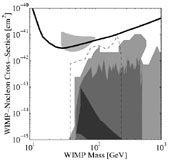
Figure 13. The elastic scattering cross section possible in the constrained MSSM [52, 56, 65] lies considerably below the range suggested by DAMA [63], which is not yet excluded by CDMS [64].

A less direct strategy is to look for the products on LSP annihilations inside the Sun or Earth. These would produce neutrinos with relatively high energies, whose interactions in rock would yield muons that could be detected in a detector deep underground, underwater [66] or in ice [67]. The prospects for detecting these muons are quite model-dependent, but it seems that annihilations inside the Sun might be more promising, at least in the benchmark scenarios [68] shown in the upper panel of Fig. 14.

Figure 14. Fluxes (upper) of muons from the core of the Sun that could be detected in a detector deep underground, underwater or in ice, and (lower) of photons from the core of the Milky Way, as calculated [68] in the proposed benchmark scenarios. The calculations are compared with the estimated sensitivities of the experiments shown.

Other suggestions have been to look for positrons or antiprotons produced by LSP annihilations in the halo of the Milky Way. Quite a large number of cosmic-ray antiprotons have now been observed, but their flux and modulation with the solar cycle are consistent with secondary production by primary matter cosmic rays. As shown here by the AMS collaboration [69], low-energy positrons in near space are also mainly produced by the collisions of cosmic rays, in the Earth's atmosphere, though there are still some hints of a possible anomaly at higher energies. However, it does not seem possible to reproduce this hint in the CMSSM [68].

Another suggestion has been to look for -ray production by annihilations in the core of the Milky Way, where the relic density may be enhanced. However, as discussed earlier, there are considerable uncertainties in this possible enhancement. Depending on its magnitude, some benchmark scenarios might offer hopes for detection in this way [68, 70], as shown in the lower panel of Fig. 14.

The general conclusion from these benchmark studies in the CMSSM is: think big! Detectors much larger than the present generation would be required to have a good chance of detecting elastic scattering, and km³ detectors are probably needed to see annihilations in the Sun or Earth.

Comments on Neutralino Scattering One of the most important contributions to spin-independent elastic scattering is that due to Higgs exchange, and one of the reasons why current predictions for the cross section are less optimistic than a few years ago is the dramatic improvement in the lower limit on the Higgs mass from LEP. The lower limit of 114.1 GeV in the Standard Model [71] also applies to the CMSSM in regions of interest for dark matter, and in the more general MSSM when tan 8 [72].

The proton and neutron structure effects on both the spin-dependent and -independent elastic scattering cross sections are relatively well under control. Despite residual uncertainties in some relevant hadronic matrix elements, other uncertainties are probably considerably larger.

Last year, the initial interpretation of the BNL experiment [73] on g_µ - 2 gave considerable hope to searches for elastic scattering, as it appeared to exclude large values of m_1/2 and m₀ [74]. However, with the recent correction of the sign of the hadronic light-by-light scattering contribution [75], the previous `discrepancy' with the Standard Model prediction for g_µ - 2 has been greatly reduced, large values of m_1/2 and m₀ are again allowed [54, 53], and the elastic scattering rate may be very small, as exemplified by the benchmark studies [68]. However, it remains true that the rate could be quite large if g_µ - 2 eventually settles down close to its present central value, and if there are no further Standard Model surprises in store.

As was discussed here, annual modulation is a potentially powerful tool for convincing skeptics that a detector signal is indeed due to the scattering of dark matter, particularly when combined with directional information [76]. The DAMA experiment is currently under pressure from a number of other experiments [64, 77, 78, 79, 80, 81, 82, 83]. In view of the possible ambiguities in the interpretation of any experimental signal, it is desirable to explore as many different techniques as possible, and it was encouraging to hear here that studies using Sodium Iodide, Germanium, Xenon, Calcium Fluoride, Lithium Fluoride and Aluminium as target materials are underway. It was also encouraging to hear that Pulse Shape Discrimination, Time Projection Chambers, Silicon Drift Detectors, and phonon-based detection strategies are being explored. It would be particularly impressive to find a confirmatory signal for spin-dependent scattering, and I recall that Fluorine is the most promising material for this purpose [84].

Axino Dark Matter As discussed here [85], the axino 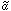is quite a `natural' possibility in an extension of the MSSM that includes an axion in order to explain why the strong interactions conserve CP. The decay constant F_a that reflects the scale of axion dynamics should be 10¹¹ GeV, so as to avoid having too much axionic cold dark matter. As in the MSSM, a plausible mass scale for the lightest neutralino is m ~ 100 GeV. Assuming these values for F_a and m, Fig. 15 displays the allowed range of the model parameter space in the m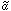, T_R plane, where T_R is the reheating temperature after inflation. As seen in Fig. 15, one must require T_R 10 TeV and m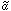 10 MeV. The latter is not a problem, since models typically yield m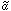 ~ 10 GeV, but in that case T_R 100 GeV would be needed, implying a somewhat unconventional cosmology.

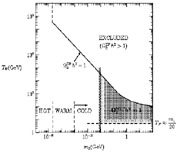
Figure 15. Compilation of constraints on axino dark matter [85], as functions of the reheating temperature TR and the axino mass m.

Gravitino Dark Matter? The thermal production of gravitinos following inflation has long been regarded as a potential problem for cosmology. To avoid this, it is generally considered that the reheating temperature cannot be too high: T_R 10⁹ GeV. In recent years, the possibility of overproducing gravitinos during inflation has also been raised [86]. As we heard here, inflatinos are certainly produced copiously, but these are not thought to convert into relic gravitinos [87].

Since gravitinos have only gravitational-strength interactions, gravitino dark matter would be unobservable, and hence a nightmare for detection experiments. In most supergravity scenarios, the gravitino weighs more than the lightest neutralino, and is unstable. However, the possibility has been raised of a light gravitino weighing ~ 1 KeV, which would be a potential candidate for warm dark matter. However, this possibility does not seem to be required, or even favoured, by cosmology, so is not pursued here.