5.2. Beyond the M - Relation: Exploring the Dark Side of Galaxies

The M - relation probes a direct connection between SBHs and galactic bulges. The velocity dispersion, , is measured within a region which, though large compared to the black hole sphere of influence, is at least an order of magnitude smaller than the optical radius of the galaxy, and is likely dominated by luminous matter (Faber & Gallagher 1979). Therefore, is unable to tell us about the connection between SBHs and other fundamental baryonic structures, such as the galactic disk or halo, while the link to the dark matter (DM) component also remains utterly unexplored.

That this issue has not yet been addressed is somewhat surprising, since it is not the mass of the bulge but rather, the total mass of the galaxy (or of the DM halo), which is the key ingredient of most theoretical models proposed for the formation of SBHs (Adams, Graff & Richstone 2000; Monaco et al. 2000; Haehnelt, Natarajan & Rees 1998; Silk & Rees 1998; Haehnelt & Kauffmann 2000; Cattaneo, Haehnelt & Rees 1999; Loeb & Rasio 1994). Once the models predict a correlation with total mass (or DM halo mass), the correlation with bulge mass is implicit because, in standard CDM scenarios, the bulge mass is loosely determined by the halo properties (e.g. van den Bosch 2000; Haehnelt, Natarajan & Rees 1998; Zhang & Wyse 2000).

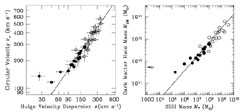
Figure 5.(left) Correlation between the rotational velocity and bulge velocity dispersion for a sample of 16 spiral galaxies (solid circles) and 21 ellipticals (open circles; plot adapted from Ferrarese 2002). Figure 6. (right) Same as Fig. 5, but with vc and converted to halo mass and black hole mass respectively (see text for further details). The upper limit on the SBH mass in M33 (Merritt et al. 2001) is shown by the arrow.

It is natural to ask whether the M - relation might just be the by-product of an even more fundamental relation between M and the total gravitational mass of the galaxy. As it turns out, such a fundamental relation is likely to exist (Ferrarese 2002). Fig. 5 demonstrates the existence of a tight correlation between the bulge velocity dispersion (the same quantity used in defining the M - relation, typically measured within an aperture of size r < ~ 0.5 kpc) and the circular velocity v_c, measured at radii r ~ 20 - 80 kpc, for a sample of 16 spiral galaxies. A regression analysis, accounting for errors in both variables, gives

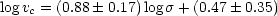
(5)

with a reduced ² of 0.64.

For spiral galaxies, v_c is measured directly from HI or optical rotation curves. In elliptical galaxies, v_c can be derived from dynamical models of the observed stellar absorption line profiles, velocity dispersion and surface brightness profiles. Fig. 5 shows that the spirals naturally blend with a sample of 21 elliptical galaxies (from Kronawitter et al. 2000) in the v_c - plane; both samples obey the relation given in equation (5).

The implications of equation (5) are exciting. The circular velocity v_c is a measure of gravitational mass through the virial theorem, and can be related to the DM halo mass (Navarro & Steinmetz 2000; Bullock et al. 2001). Keeping in mind that, as discussed in section 5.1, the M - relation is not well defined below 10⁷ M, and not defined at all below 10⁶ M, the v_c - relation can be translated into a relation between the mass of the central black hole (related to through equation 2) and that of the DM halo (Fig. 6):

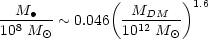
(6)

(Ferrarese 2002). The existence of this relation seems to conflict with recent claims that SBHs do not relate to any other galactic structure but the bulge (Richstone et al. 1998; Kormendy & Gebhardt 2001; Gebhardt et al. 2001).

The relation between M and M_DM is non-linear, with the ratio M / M_DM decreasing from 6 × 10^-5 for M_DM ~ 10¹⁴ M, to 5 × 10^-6 for M_DM ~ 10¹² M. Haehnelt, Natarajan & Rees (1998) advocated a nonlinear relation between SBH and DM halo mass in order to reproduce the luminosity function of QSOs, noting that a linear relation would translate into too low a value for the QSO duty cycle, t_QSO ~ 3 × 10⁵ yr. Increasing the QSOs lifetime to values more in line with current observational constraints (e.g. Martini & Weinberg 2001) produces an increasingly steeper relation between M and M_DM. If t_QSO ~ 1.5 × 10⁷ yr (equal to the Salpeter time), then the slope of the M - M_DM relation must be increased to ~ 2 to provide a reasonable fit to the QSO luminosity function. The empirical correlation shown in Fig. 6 seems to support such claims. Furthermore, Fig. 6 indicates that the tendency of massive halos to become less efficient in forming SBH as M_DM decreases, is even more pronounced for halos with M_DM < 10¹² M, and breaks down completely in the case of M33. Such halos might indeed be unable to form SBH, as proposed on theoretical grounds by Haehnelt, Natarajan & Rees (1998) and Silk & Rees (1998).