Generically topological defects will be produced if the conditions for their existence are met. Then for example if the unbroken group H contains a disconnected part, like an explicit U(1) factor (something that is quite common in many phase transition schemes discussed in the literature), monopoles will be left as relics of the transition. This is due to the fundamental theorem on the second homotopy group of coset spaces [Mermin, 1979], which states that for a simply-connected covering group G we have (5)
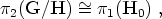
| (4) |
with H0 being the component of the unbroken group
connected to the identity. Then we see that since monopoles are
associated with unshrinkable surfaces in G/H, the
previous equation implies their existence if H is
multiply-connected. The reader may guess what the consequences are
for GUT phase transitions: in grand unified theories a semi-simple
gauge group G is broken in several stages down to
H = SU(3) × U(1). Since in this case
1(H)
,
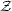the integers, we have
2 (G /
H) 
1 and
therefore gauge monopole solutions exist
[Preskill, 1979].
5 The isomorfism between two groups is
noted as
. Note that by using
the theorem we therefore can reduce the computation of
2 for a
coset space to the computation of
1 for a group. A
word of warning: the focus here is on the physics and the
mathematically-oriented reader should bear this in mind, especially
when we will become a bit sloppy with the notation. In case this
happens, consult the book
[Steenrod, 1951]
for a clear exposition of these matters.
Back.