2.6. Evolution of global textures

We mentioned earlier that the breakdown of any non-Abelian global symmetry led to the formation of textures. The simplest possible example involves the breakdown of a global SU(2) by a complex doublet ^a, where the latter may be expressed as a four-component scalar field, i.e., a = 1 ... 4. We may write the Lagrangian of the theory much in the same way as it was done in Eq. (1.7), but now we drop the gauge fields (thus the covariant derivatives become partial derivatives). Let us take the symmetry breaking potential as follows, V() = /4 (||² - ²)². The situation in which a global SU(2) in broken by a complex doublet with this potential V is equivalent to the theory where SO(4) is broken by a four-component vector to SO(3), by making ^a take on a vacuum expectation value. We then have the vacuum manifold given by SO(4) / SO(3) = S³, namely, a three-sphere with ^a _a = ². As ₃ (S³) 1 (in fact, ₃ (S³) = 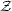) we see we will have non-trivial solutions of the field ^a and global textures will arise.

As usual, variation of the action with respect to the field ^a yields the equation of motion

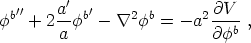
(15)

where primes denote derivatives with respect to conformal time and is computed in comoving coordinates. When the symmetry in broken three of the initially four degrees of freedom go into massless Goldstone bosons associated with the three directions tangential to the vacuum three-sphere. The `radial' massive mode that remains (m ~ ^1/2 ) will not be excited, provided we concentrate on length scales much larger than m^-1.

To solve for the dynamics of the field ^b, two different approaches have been implemented in the literature. The first one faces directly the full equation (15), trying to solve it numerically. The alternative to this exploits the fact that, at temperatures smaller than T_c, the field is constrained to live in the true vacuum. By implementing this fact via a Lagrange multiplier ⁽¹³⁾ we get

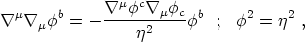
(16)

with ^µ the covariant derivative operator. Eq. (16) represents a non-linear sigma model for the interaction of the three massless modes [Rajaraman, 1982]. This last approach is only valid when probing length scales larger than the inverse of the mass m^-1. As we mentioned before, when this condition is not met the gradients of the field are strong enough to make it leave the vacuum manifold and unwind.

The approach (cf. Eqs. (16)) is suitable for analytic inspection. In fact, an exact flat space solution was found assuming a spherically symmetric ansatz. This solution represents the collapse and subsequent conversion of a texture knot into massless Goldstone bosons, and is known as the spherically symmetric self-similar (SSSS) exact unwinding solution. We will say no more here with regard to the this solution, but just refer the interested reader to the original articles [see, e.g., Turok & Spergel, 1990; Notzold, 1991]. Simulations taking full account of the energy stored in gradients of the field, and not just in the unwinding events, like in Eq. (15), were performed, for example, in [Durrer & Zhou, 1995]. ⁽¹⁴⁾

⁽¹³⁾ In fact, in the action the coupling constant of the `Mexican hat' potential is interpreted as the Lagrange multiplier. Back.

⁽¹⁴⁾ Simulations of the collapse of `exotic' textures can be found at http://camelot.mssm.edu/~ats/texture.html Back.