6.4. More cosmological miscellanea
Regarding vortons, their presence and evolution was recently the subject of much study, and grand unified models producing them were confronted with standard cosmological tests, as the primordial nucleosynthesis bounds and the dark matter content in the universe today [Carter & Davis, 2000]. Without entering into too much detail, in order for the density of vortons at temperatures roughly around 10 MeV not to affect nucleosynthesis results for the light elements, the maximum energy scale for current condensation cannot exceed 105 GeV. This is a limit for approximately chiral vortons, where the velocity of the carriers approaches that of light, and constitutes a much more stringent bound that for nonchiral states. For this result, the analysis demanded just that the universe be radiation dominated during nucleosynthesis. For long-lived vortons the requirement is stronger, in the sense that this hypothetical population of stable defects should not overclose the present universe. Hence, present dark matter bounds also yield bounds on vortons and these turn out to be comparable to the nucleosynthesis ones. Although these results are preliminary, due to the uncertainties in some of the relevant parameters of the models, grand unified vortons seem to be in problems. On the other hand, vortons issued from defects formed during (or just above) the electroweak phase transition could represent today a significant fraction of the nonbaryonic dark matter of the universe.
Fermionic zero modes may sustain vorton configurations. In grand unified models, like SO(10), where the symmetric phase is restored in the interior of the string, there will be gauge bosons in the core. If vortons diffuse after a subsequent phase transition these bosons will be released and their out-of-equilibrium decay may lead to a baryon asymmetry compatible with nucleosynthesis limits [Davis & Perkins, 1997; Davis, et al., 1997]. Another recent mechanism for the generation of baryon asymmetry, this time at temperatures much lower than the weak scale, takes advantage of the fact that superconducting strings may act like baryon charge `bags', protecting it against sphaleron effects [Brandenberger & Riotto, 1998].
The above mentioned bounds on vortons can be considerably weakened if,
as we showed before, electromagnetic corrections to the string
equation of state are properly taken into account. In other words, a
proto-loop can become a vorton only provided certain relations
between the values of the conserved parameters characterizing the
vorton hold. We have seen that these relations (embodied in the
relevant master function of the string) change whenever
electromagnetic self couplings are considered.
A given distribution of vortons will be characterized by the ratio of
the conserved numbers b
N / Z. As
it turns out, increasing the
electromagnetic correction is equivalent to reducing the available
phase space for vorton formation, as b of order unity is the most
natural value [see, e.g.,
Brandenberger, Carter,
Davis & Trodden, 1996]
situation that we sketch in Figure 1.24. On this
figure, we have assumed a sharply peaked dN / db
distribution centered around b = 1; with
q2
= 0, the available range for vorton
formation lies precisely where the distribution is maximal, whereas
for any other value, it is displaced to the right of the
distribution. Assuming a Gaussian distribution, this effect could
easily lead to a reduction of a few orders of magnitude in the
resulting vorton density, the latter being proportional to the area
below the distribution curve in the allowed interval. This means that
as the string loops contract and loose energy in the process, they
keep their `quantum numbers' Z and N constant, and some
sets of
such constants which, had they been decoupled from electromagnetism,
would have ended up to equilibrium vorton configurations, instead
decay into a bunch of Higgs particles, themselves unstable. This may
reduce the cosmological vorton excess problem if those are
electromagnetically charged.
|
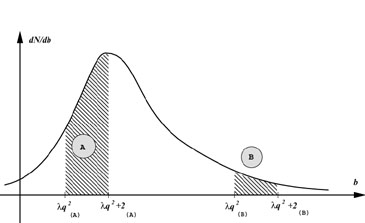
Figure 1.24. A possible way out of the
vorton excess problem: a sketch of a
distribution of loops with b
|
The cosmic microwave background radiation might also be used as a
charged string loop detector. In fact vortons are like point masses
with quantized electric charge and angular momentum. They are
peculiar for, if they are formed at the electroweak scale, their
characteristic size cannot be larger than a hundredth the classical
electron radius, while their mass would be some five orders of
magnitude heavier than the electron. They can however contain up to
-1 ~ 137
times the electron charge, and hence Thomson
scattering between vortons and the cosmic background radiation at
recombination would be (we are admittedly optimistic in here) just nearly at
the same level as the standard one, with important consequences for,
e.g., the polarization of the relic radiation. The signature would
depend on the actual distribution of relic vortons at z ~ 1000, an
input that is presently largely unknown. According to current
estimates [e.g.,
Martins & Shellard,
1998b],
electroweak vortons could
contribute non-negligibly to the energy density. However, current
figures are still well below what is needed to get a distinguishable
signal from them and thus their CMB trace would be hidden in the `noise'
of the vastly too numerous electrons.
Acknowledgments
For these lectures I've drawn freely from various sources. I thank the people who kindly provided figures and discussions. Among them, I owe special debts to Brandon Carter, Jérôme Martin, Patrick Peter, Levon Pogosian, and Serge Winitzki for very enjoyable recent collaborations. Thanks also to the other speakers and students for the many discussions during this very instructive study week we spent together, and to the members of the L.O.C. for their superb job in organizing this charming school. A.G. thanks CONICET, UBA and Fundación Antorchas for financial support.