Copyright © 1999 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1999. 37:
487-531 Copyright © 1999 by Annual Reviews. All rights reserved |
3.2. General Abundance Analysis
Abundance estimates from absorption lines are, in principle, more straightforward than for emission lines because the absorption strengths are not sensitive to the temperatures or space densities in the gas. Moreover, absorption lines yield direct measures of the column densities in different ions. We need only apply appropriate ionization corrections to convert the column densities into relative abundances. For example, the abundance ratio of any two elements a and b can be written,
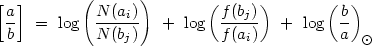 |
(10) |
which is identical to Equation 8 except that the Ns here are the
column densities. Once again we define the ionization correction as
IC  log(f (bj) /
f (ai)). Abundance studies would ideally compare
lines with similar
ionizations to minimize IC and reduce the sensitivity
to potentially complex geometries. Unfortunately, the lines available
often require significant ionization corrections. In particular, we are
often forced to compare highly ionized metals (such as CIV) to HI
(Ly
log(f (bj) /
f (ai)). Abundance studies would ideally compare
lines with similar
ionizations to minimize IC and reduce the sensitivity
to potentially complex geometries. Unfortunately, the lines available
often require significant ionization corrections. In particular, we are
often forced to compare highly ionized metals (such as CIV) to HI
(Ly ) to
derive the metallicity. We must therefore use ionization models.
) to
derive the metallicity. We must therefore use ionization models.
The usual assumption is that the gas is photoionized by the QSO continuum flux. Collisional ionization would lead to lower derived metallicities because it creates less HI (and more HII) for a given level of ionization in the metals (cf Figures 4 and 5 in Hamann et al. 1995; see also Turnshek et al. 1996). However, collisional ionization has been generally dismissed for BAL regions (BALRs) because (a) it would be energetically hard to maintain, (b) it would produce excessive amounts of line emission (because of the much higher temperatures), and (c) it is hard to reconcile with the observed simultaneous variabilities in BAL troughs across a wide range of velocities (Weymann et al. 1985, Junkkarinen et al. 1987, Barlow 1993). In contrast, the strong radiative flux known to be present in QSOs provides a natural ionization source. We will assume that photoionization dominates in both BALRs and intrinsic NALRs.
Estimates of IC generally come from plots like Figure 10, which shows the ionization fractions of HI and various metal ions Mi in photoionized clouds (see Section 2.5 and Ferland et al. 1998 for general descriptions of the calculations). Ideally, we would compare column densities in different ions of the same element to obtain abundance-independent constraints on the ionization and thus IC. Otherwise, column densities in different elements can also constrain IC with assumptions about their relative abundances.
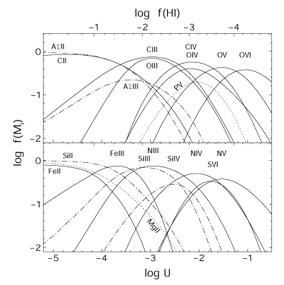 |
Figure 10. Ionization fractions in
optically thin clouds photoionized by a power-law spectrum with
|
Note that the results in Figure 10 are not sensitive to the particular abundances used in the calculations (in this case solar), so the figure is useful for general abundance/ionization estimates (see Hamann 1997). The model clouds are optically thin in the ionizing UV continuum, which means that gradients in the ionization are negligible across the cloud and the ionization fractions do not depend on the total column densities. This simplification appears to be appropriate for most intrinsic absorption line systems (based on their measured column densities), although shielding by many far-UV BALs might affect the ionization structure downstream in BALRs (Korista et al. 1996, Turnshek 1997, Hamann 1997). Also, systems with low-ionization lines like FeII or MgII can be optically thick at the HI Lyman edge (Bergeron & Stasinska 1986, Voit et al. 1993, Wampler et al. 1995) and may require calculations with specific column densities that match the data.
The main theoretical uncertainties involve the shape of the ionizing spectrum, the frequent lack of ionization constraints (too few lines measured), and the possibility of inhomogeneous (multizone) absorbing regions. Hamann (1997) addressed these issues by calculating IC values for a wide range of conditions in photoionized clouds. He noted that, whenever there is or might be a multizone absorber with a range of ionization states, we can still make conservatively low estimates of the metal-to-hydrogen abundance ratios by assuming each metal line forms where that ion is most favored - that is, at the peak of its ionization fraction f(Mi) in Figure 10. We can also place firm lower limits on the metal-to-hydrogen ratios by adopting the minimum values of IC, which correspond to minima in the f(HI) / f(Mi) ratios (see also Bergeron & Stasinska 1986). The lower limits are robust, even though they come from one-zone calculations, because the presence of different or additional zones can only mean that larger IC values are appropriate for the data. Figure 11 plots several minimum metal-to-hydrogen ICs for optically thin clouds photoionized by different power-law spectra. The results in this plot simply get added to the logarithmic column density ratios (Equation 10) to derive minimum metallicities. Note that some important metal-to-metal ratios also have minimum IC values, such as PV/CIV and FeII/MgII (Hamann 1998; F Hamann, R Chaffee, RJ Weymann, TA Barlow, VT Junkkarinen, manuscript in preparation).
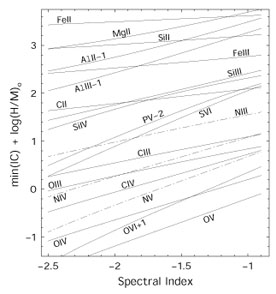 |
Figure 11. Minimum metal ion-to-HI
ionization corrections (IC) normalized to solar abundances (the
last two terms in Equation 10) are
plotted for optically thin clouds photoionized by power-law spectra with
different indices ( |
3.2.2. Column Densities and Partial Coverage
The final critical issue is deriving accurate column densities from the absorption troughs. In the simplest case, the optical depths in well-resolved lines are related to the observed intensities by,
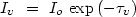 |
(11) |
where Iv and Io are the observed and
intrinsic (unabsorbed) intensities, respectively, and
 v is the
line optical depth, at each
velocity shift v. The column densities follow from the
optical depths by,
v is the
line optical depth, at each
velocity shift v. The column densities follow from the
optical depths by,
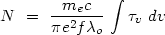 |
(12) |
where f is the oscillator strength and
 o is the
laboratory wavelength
of the line. Column density derivations can involve line profile fitting
or direct integration over the observed profiles (via Equations 11 and 12,
Junkkarinen et al.
1983,
Grillmair & Turnshek
1987,
Korista et al. 1992,
Savage & Sembach
1991,
Jenkins 1996,
Arav et al. 1999).
Very optically thick lines are not useful because the inferred values of
o is the
laboratory wavelength
of the line. Column density derivations can involve line profile fitting
or direct integration over the observed profiles (via Equations 11 and 12,
Junkkarinen et al.
1983,
Grillmair & Turnshek
1987,
Korista et al. 1992,
Savage & Sembach
1991,
Jenkins 1996,
Arav et al. 1999).
Very optically thick lines are not useful because the inferred values of
 v are far too
sensitive to uncertainties in Iv. In other cases, the
analysis might still be compromised by
(a) unresolved absorption line components or (b)
unabsorbed flux that fills in the bottoms of the observed
troughs. If either of these
possibilities occurs, the derived optical depths and column densities
become lower limits, and the derived abundances become incorrect.
Errors from the first possibility can always be reduced or avoided by
higher-resolution spectroscopy.
v are far too
sensitive to uncertainties in Iv. In other cases, the
analysis might still be compromised by
(a) unresolved absorption line components or (b)
unabsorbed flux that fills in the bottoms of the observed
troughs. If either of these
possibilities occurs, the derived optical depths and column densities
become lower limits, and the derived abundances become incorrect.
Errors from the first possibility can always be reduced or avoided by
higher-resolution spectroscopy.
The second possibility, of filled-in absorption troughs, is actually an asset for identifying intrinsic NALs (Section 3.1). We refer to this filling-in generally as partial coverage of the background emission source(s). Figure 12 shows several geometries that might produce partial coverage and filled-in troughs. (3) (The situation can be potentially more complicated if the absorber itself is a source of emission. The analysis discussed below remains the same, however.) When partial coverage occurs, the observed intensities depend on both the optical depth and the line-of-sight coverage fraction, Cf, at each velocity,
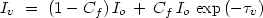 |
(13) |
where 0  Cf
Cf
 1, and the first
term on the right side is the unabsorbed (or uncovered)
contribution. Measured absorption lines can thus be shallow even when
the true optical depths are large. In the limit
1, and the first
term on the right side is the unabsorbed (or uncovered)
contribution. Measured absorption lines can thus be shallow even when
the true optical depths are large. In the limit
 v >> 1, we have
v >> 1, we have
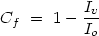 |
(14) |
Outside of that limit, we can compare lines whose true optical-depth
ratios are fixed by atomic physics, such as the HI Lyman lines or doublets
like CIV 
 1548,1550, SiIV
1548,1550, SiIV

 1394,1403 etc, to determine
uniquely both the coverage fractions and the true optical depths
across the line profiles (Hamann 1997b,
Barlow & Sargent
1997,
Arav et al. 1999,
Srianand &
Shankaranarayanan 1999,
Ganguly et al. 1999).
For example, a little algebra shows that for
doublets with true optical-depth ratios of ~ 2 (as in CIV, SiIV, etc), the
coverage fraction at each absorption velocity is,
1394,1403 etc, to determine
uniquely both the coverage fractions and the true optical depths
across the line profiles (Hamann 1997b,
Barlow & Sargent
1997,
Arav et al. 1999,
Srianand &
Shankaranarayanan 1999,
Ganguly et al. 1999).
For example, a little algebra shows that for
doublets with true optical-depth ratios of ~ 2 (as in CIV, SiIV, etc), the
coverage fraction at each absorption velocity is,
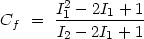 |
(15) |
where I1 and I2 are the observed
line intensities, normalized by
Io, at the same velocity in the weaker- and
stronger-line troughs, respectively. The corresponding line optical depths
are  2 =
2
2 =
2 1 and
1 and
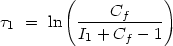 |
(16) |
It is a major strength of the NALs that we can resolve key multiplet lines and use this analysis to measure the coverage fractions, thus deriving reliable column densities and abundances. It is a great weakness of the BALs that this analysis is usually not possible because the lines are blended. We will argue below that BAL studies so far have been seriously compromised by unaccounted for partial-coverage effects.
The only drawback of partial coverage for the NALs is that there might be a range of coverage fractions in multizone-absorbing media. There is already evidence in some cases for coverage fractions that differ between ions or change with velocity across the line profiles (Barlow & Sargent 1997, Barlow et al. 1997, Hamann et al. 1997b). Variations in Cf with velocity can always be dealt with by analyzing limited velocity intervals in the line profiles (see also Arav 1997). But one can imagine complex geometries where ionization-dependent coverage fractions would jeopardize the simple abundance analysis described above, in particular for comparisons between high- and low-ionization species like CIV and HI. Abundance ratios based on disparate species like these might require specific models of the ionization-dependent coverage. On the other hand, this worst-case scenario is not known to occur, and there is no reason to believe it would lead to generally overestimated metallicities anyway.
3 The situation can be potentially more complicated if the absorber itself is a source of emission. The analysis discussed below remains the same, however. Back.