3.3. Elliptical and cD Galaxies

3.3.1. Three-Dimensional Shapes

Renewed interest in the three-dimensional shapes of elliptical galaxies stems from the recent revision in our picture of E-galaxy dynamics (see section 4). The observation that ellipticals rotate less than they would if they were rotationally flattened has led to the realization that their velocity distributions are anisotropic and hence that they may be triaxial. Photometric evidence reviewed in this section confirms that many ellipticals are triaxial, and suggests that this triaxiality is frequently tidal in origin.

The classical way to study the shapes of galaxies is to infer the distribution of true axial ratios from the distribution of apparent shapes on the assumption that galaxies are oriented randomly (e.g., Hubble 1926; Sandage, Freeman and Stokes 1970). The most thorough study of this kind is that of Binney and de Vaucouleurs (1981). They use the large sample of the RC2 and a non-parametric inversion technique (i.e., they do not constrain the functional form of the intrinsic shape distribution). A restricted range of triaxial forms is also considered. Then, if elliptical galaxies are oblate spheroids, the most common intrinsic shape is found to be E3.5 - 3.8, with a significant number of spherical objects, and none flatter than E6.5. This essentially confirms results of Sandage, Freeman and Stokes (1970) and of de Vaucouleurs (1959a, 1974a, 1977). There appears to be little dependence of the intrinsic shape on luminosity. Any such dependence is opposite in sense to the prediction of tidal torque theories of the origin of galactic rotation (e.g., Thuan and Gott 1977); more luminous galaxies are, if anything, flatter than fainter galaxies (van den Bergh 1977a; Strom and Strom 1978a, b, c, d; Efstathiou and Ellis 1978). If ellipticals are prolate spheroids, the preferred shape found by Binney and de Vaucouleurs is again E3.8, with none flatter than E6 and with more spherical objects than in the oblate case (see also Binney 1978a). Triaxial shapes of many kinds are allowed. The apparent axial ratio distribution does not put useful constraints on the fractions of ellipticals which are oblate and prolate, a conclusion also emphasized by Binggeli (1980).

More specific tests to distinguish prolate and oblate galaxies use the observed correlations between ellipticity and characteristic surface brightness or central velocity dispersion. Marchant and Olson (1979), Richstone (1979a, b) and Olson and de Vaucouleurs (1981) have exploited the fact that galaxies have their highest surface brightnesses when the viewing path length through them is longest. Thus oblate objects appear brightest when they are seen edge-on, i.e., when they appear flattest. Prolate objects look brightest when they are seen end-on and therefore most nearly round. All three groups above find that surface brightnesses are higher in more flattened ellipticals than in nearly round ones. All three correlations, representing different galaxy samples and different kinds of characteristic surface brightness, are statistically significant. These results suggest that ellipticals are predominantly oblate. Lake (1979) has proposed a similar test based on apparent central velocity dispersions. For samples of prolate and oblate galaxies, these should be largest in those objects which appear roundest and flattest, respectively. The available data weakly favor prolate models. However, both kinds of tests suffer from problems which make them less than convincing. Both are invalid if there exist intrinsic correlations between galaxy shape and volume emissivity or velocity dispersion. In fact, such a correlation is now known to exist for velocity dispersions. Terlevich et al. (1981) have shown that flatter ellipticals have smaller dispersions, a result which mimics the behavior of prolate objects (cf. Lake's preliminary result). Thus, although the above photometric test favors oblate models, there is great freedom in the distribution of intrinsic shapes. It is certainly possible that some ellipticals are prolate.

Direct photometric evidence for triaxiality is provided by observations that the major-axis position angles in some ellipticals twist with increasing radius. A galaxy showing isophote twists cannot be spheroidal, nor can it consist of similar ellipsoids. A twist can imply that the true principal axes change position angle with radius. However, Binney (1978b; Mihalas and Binney 1981, pp. 331-333) has pointed out that a simpler model is sufficient. The galaxy can consist of triaxial isodensity surfaces whose principal axes are aligned, but whose axial ratios change with radius. Figure 6 illustrates this point. Isophote twists have been observed in ellipticals for many years (e.g., Liller 1960, 1966), but King (1978) was the first to emphasize the implication that ellipticals are probably triaxial. He detected significant twists, generally 10°-20°, in five of sixteen galaxies studied. The almost simultaneous discovery that ellipticals rotate very slowly, which is also naturally interpreted in terms of a triaxial structure, led to a flurry of interest in searching for twists. These were found in three of four galaxies studied by Williams and Schwarzschild (1979a, b), 40% of 15 ellipticals surveyed by Carter (1978, 1979), 47% of 75 ellipticals surveyed by di Tullio (1979) and 55% of 31 ellipticals measured by Leach (1981). The feeling has therefore developed that photometry confirms the kinematic results, implying that most ellipticals are triaxial. Problems with this belief are discussed later in this section.

Figure 6. Two-dimensional analogue of "isophote twisting without isophote twisting" in elliptical galaxies. The upper panel is a face-on view (left and center) of two isophotes with different ellipticities and (right) of a galaxy consisting of isophotes with different ellipticities but a single position angle. In the lower panel the same configurations are viewed at an angle. When flat ellipses are viewed at skew orientations, projection effects make the apparent major axes (ticks) rotate away from the intrinsic major axes (straight lines) toward the line (dashed) about which the objects have been rotated to produce the viewing geometry. The change in apparent position angle is larger for isophotes which are more nearly round. This produces a twist in the position angle with radius for any model galaxy (lower right) consisting of dissimilar isophotes, even if those isophotes are really aligned. A similar effect exists for three-dimensional objects which are triaxial.

More detailed studies have begun to set useful constraints on how triaxial ellipticals can be. Several studies have shown that the total twist angle correlates with apparent ellipticity (Galletta 1980; Benacchio and Galletta 1980; Leach 1981). Galaxies which are very flattened ( > 0.25) show only small twists ( 20°). Galaxies which are nearly round can show small or large twists. Considerable caution is required in interpreting these - correlations because of the possibility that some SB0 galaxies are included. This is clearly the case for the Strom and Strom (1978a, b, c) sample, which provides most of the data used by Galletta (1980) and by Benacchio and Galletta (1980). S0 galaxies were specifically not excluded, and an examination of the objects reveals many SB0s. Nevertheless, the general behavior of the published - diagrams is probably correct. Benacchio and Galletta (1980) have made an interesting first attempt to study the distribution of intrinsic shapes based on such data. They project at random orientations various distributions of triaxials to simultaneously fit (1) the distribution of points in the - diagram, and (2) the observed distribution of axial ratios. The best fit is obtained for models which are mildly triaxial, with principal axes a, b, c in the ratios b/a 0.81 ± 0.04 (dispersion) and c/a 0.62 ± 0.13, under the (arbitrary) restriction that b/a = 0.31 (c/a) + 0.62. These results are still only indicative because of the above problems with the data. However, the machinery developed in Benacchio and Galletta (1980) is useful, and should yield stricter limits on galaxy shapes when applied to more accurate measurements of a larger sample of galaxies (see also Leach 1981).

Although statistical studies of galaxy shapes are useful, the immediate need is to obtain both kinematic and photometric data in a few objects to allow realistic modeling. Some progress in this direction is provided by Williams' (1981) photometric and kinematic study of the E2P galaxy NGC 596. This was known to be an interesting object because Schechter and Gunn (1978) observed rotation velocities as large as ~ 90 km s^-1 at r ~ 15" along the minor axis of the outer isophotes. Williams measured stellar rotation along six slit positions through the nucleus. He confirms that the kinematic major axis at r ~ 13" radius has a position angle of 120° ± 4°, coincident with the minor axis at r ~ 50". The photometric major axis near the center is at position angle 90°, about 30°; away from the kinematic major axis. There is therefore a twist of ~ 60° in the isophotes, most of which occurs outside the region studied kinematically. The degree of triaxiality needed to explain these observations is surprisingly small. Williams makes a crude deprojection of the photometry under the simplifying assumption that there is no intrinsic twist and the plausible assumption that one principal axis is the rotation axis. The free parameters are the two remaining orientation angles and the axial ratios b/a and c/a as a function of radius. For various values of the orientation angles, a variety of triaxial forms is consistent with the photometry. In all of them the rotation axis is the longest axis at large radii. Both prolate and oblate configurations are allowed; some models are oblate near the center and prolate at large radii. Rarely is an axial ratio b/a or c/a smaller than 0.5. Like the Benacchio and Galletta (1980) work, Williams' study gives valuable indications regarding the shapes of ellipticals, and useful machinery with which to attack more complete data.

Despite the increasing success of studies like the above, great caution is required in the interpretation of isophote twists. The accuracy of some published data is not very good. For example, it is relatively easy to produce twists by incorrectly accounting for halos of nearby stars and galaxies. Also, the problem of contamination of samples by SB0s has already been mentioned. The most important caveat, which I would like to discuss at length, is the growing evidence that many twists found to date are not intrinsic but are the result of tidal effects.

It is widely assumed that twists can be caused tidally. The best-known example is NGC 205 (Fig. 7), in which Hodge (1973) has found a twist of at least 30° toward M31. Examination of published surveys shows that the occurrence of twists correlates strongly with the presence of companions. For example, di Tullio (1979) finds that all 34 galaxies in which she detects significant twists > 10° are in pairs, groups or clusters. Thirty of the 34 have asymmetries in their isophotes. Twenty galaxies in her sample have small companions in their envelopes and all of them have both twists and asymmetries. To investigate such correlations with companions it is convenient to use the tidal classes of Kormendy (1977c), illustrated here in Figures 8 - 10. Essentially, T3 galaxies are ones with companions that are so prominent that tidal effects are very probable. T1 galaxies are isolated enough to probably be unperturbed. T2 galaxies are intermediate. Examination of galaxies with significant twists shows that T3 galaxies account for three of five in King (1978), two of three in Williams and Schwarzschild (1979a, b), and a majority of the galaxies in Carter (1978). The importance of companions can be illustrated more quantitatively using a detailed study of twists by Leach (1981). In this paper, characteristic values for the change in ellipticity ^* and the twist ^*, both per unit effective radius r_e (see section 3.3.2) are given for 31 bright ellipticals. Of the eight galaxies showing very large twists ^* > 10°r_e^-1, only one is isolated (NGC 3078, a T1); one is T2 and the other six are T3. These six galaxies are illustrated in Figures 9 and 10. The seven T1 galaxies in the sample mostly show small twists ^* < 5°r_e^-1 (the main exception is NGC 3078). Four of these objects are illustrated in Figure 8. Table 2 summarizes the average values of the twists and ellipticity changes. Both are larger in T3 than in T1 galaxies. In an attempt to minimize measuring problems, I also show in Table 2 the results for galaxies with 0.2. The sample is reduced, as is the average twist (this is just the - correlation). However, T3 galaxies still show larger ellipticity and position angle changes than T1 objects. None of the differences are statistically strong. However, the data are suggestive of tidal effects. Two final illustrations are given in Figure 10. NGC 596, whose probable triaxiality was discussed above, turns out to be a T2 galaxy. NGC 3379, an obviously T3 object, shows not only a twist of ~ 10°, but also a displacement of the centers of the outer isophotes with respect to the inner structure; this behavior is shared by the companion NGC 3384 (Barbon, Benacchio and Capaccioli 1976, Fig. 3). I do not mean to imply that all twists in T3 galaxies are tidal. Some may be due to photometry problems with overlapping isophotes. Some are certainly intrinsic. However, the above observations suggest that tidal effects may account for most large twists detected to date. Thus the unambiguous photometric evidence for triaxiality in ellipticals is less extensive than is commonly believed.

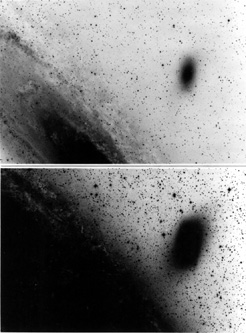Figure 7. Twisting of the outer isophotes of NGC 205 toward M31. The light exposure is from an 8 min 103a-0 + GG13 plate taken with the 1.2m Palomar Schmidt telescope. The deep photograph is from a 90 min IIIa-J + Wr 2c Palomar Schmidt plate taken and kindly made available by S. van den Bergh.

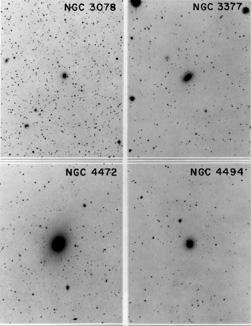Figure 8. Isolated galaxies with (mostly) small twists. These galaxies have no companions which are close enough to plausibly cause tidal effects; they illustrate the T1 tidal class of Kormendy (1977c). Their twists are * = 13.6°re-1 in NGC 3078, 1.7°re-1 in NGC 3377, 4.6°re-1 in NGC 4472 and 0.7°re-1 in NGC 4494 (Leach 1981).

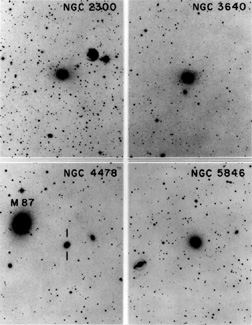Figure 9. Four of the eight galaxies which show the largest twists in Leach (1981). These galaxies illustrate the T3 tidal class; they have companions of comparable luminosity within one or two diameters. Tidal effects are therefore likely to be important (subject to possible projection effects). There is some tradeoff in the classification between relative luminosity and separation; e.g., galaxies such as NGC 5846 which have small companions well inside their envelopes are also T3. The twist values are * = 13.2°re-1 in NGC 2300, 17.6°re-1 in NGC 3640, 13.5°re-1 in NGC 4478 and 20.0°re-1 in NGC 5846.

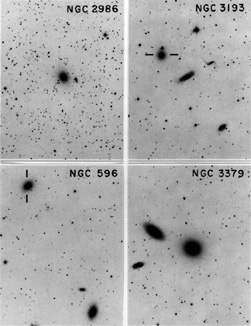Figure 10. The upper panels show the galaxies with the largest twists in Leach (1981). Both are T3 objects. NGC 596 (Williams 1981) is a relatively isolated T2 (lower left). NGC 3379 (lower right) is a T3 galaxy with both a twist and a displacement of ~ 2" of the outer with respect to the inner isophotes. These effects are probably not due to problems with overlapping isophotes, since the separation from NGG 3384 (the upper companion) is ~ 450", while the measurements of Barbon et al. (1976) extend only to r ~ 135" (µ = 24.3 B mag arcsec-2).

Table 2. correlation with companions of twists and ellipticity changes

Sample	n	<*>	<*>
T1	7	0.032 ± 0.015	4.6° ± 1.8°
T2	11	0.063 ± 0.016	4.2° ± 1.3°
T3	11	0.059 ± 0.015	8.7° ± 2.0°
T1; 0.2	3	0.04 ± 0.04	1.6° ± 0.7°
T2; 0.2	7	0.05 ± 0.01	4.3° ± 1.9°
T3; 0.2	5	0.08 ± 0.03	4.6° ± 2.5°
NOTES. - The number of ellipticals in each sample is n. < *> and <*> are averages of the absolute values of the ellipticity and major-axis position-angle changes per unit effective radius re. Estimated errors in the means are quoted. The data are taken from Table 1 of Leach (1981), which omits two galaxies with exceptionally large twists. Both are T3 objects. NGC 4379, an S0, is also omitted.