


3.3.3. Characteristic Parameters of Elliptical Galaxies
The pioneering study of characteristic parameters of elliptical
galaxies was made by
Fish (1964).
For 29 ellipticals with photometry
available he found that the total luminosity L
 re2. Values of Ie
were not generally available, but since L
re2. Values of Ie
were not generally available, but since L
 Ie re2 for an
r1/4 law, we
infer that Ie = constant for all galaxies. Under the
assumption that
the mass-to-light ratio M/L is also constant, Fish derived the
dynamically interesting consequence, namely that the potential energy
Ie re2 for an
r1/4 law, we
infer that Ie = constant for all galaxies. Under the
assumption that
the mass-to-light ratio M/L is also constant, Fish derived the
dynamically interesting consequence, namely that the potential energy

 M3/2. He then explored the physical processes that
went on during galaxy formation, concluding that the collapse of gaseous
protogalaxies was halted by the development of internal opacity.
M3/2. He then explored the physical processes that
went on during galaxy formation, concluding that the collapse of gaseous
protogalaxies was halted by the development of internal opacity.
Better and more extensive data are now available. These show that the above relations need revision. Ie is not the same for all galaxies. Instead, there is a good correlation between Ie and re, shown in Figure 13. This has the form (Kormendy 1980)
 |
(6) |
The parameter along this line is absolute magnitude MB; lines of constant MB have slope 5 in Figure 13. On average, more luminous galaxies have larger re and fainter Be (see also Oemler 1976; Strom and Strom 1978a, b, c, 1979b). Using MB = Be - 5 log re + constant gives
 |
(7) |
The scatter about those relations is large, since lines of constant MB are almost parallel to the Be - log re relation. The implications of this result on theories of galaxy formation have not been explored. Some recent work along the lines of Fish's study has been published by Saito (1979), and Silk and Norman (1981).
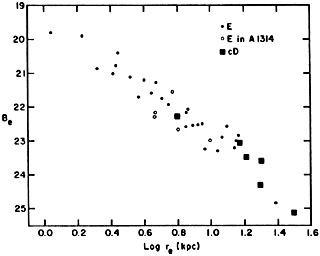 |
Figure 13. Be versus log
re for 29 elliptical galaxies in poor
clusters, from photometry by
Kormendy (1977a),
King (1978) and
Williams and Schwarzschild (1979a,
b).
Three S0 galaxies with almost negligible
disks are included. The straight line is a least-squares fit (equation
6) to these points. Also shown are parameters for cD galaxies and for
ellipticals in the cluster A1314
(Oemler 1976).
Oemler's V magnitudes
have been transformed to B by assuming B-V = 1.00. All
r1/4-law
parameters discussed in this paper refer to the mean profile, i.e., the
profile along a line oriented at 45° to the major
axis. Distances to nearby ellipticals have been derived using
H0 = 50 km s-1 Mpc-1;
relative distances to A1314 and to the cDs are calculated assuming a
Hubble constant larger by a factor of 1.46
(Aaronson et al. 1980),
corresponding to |
The above discussion is unchanged from
Kormendy's (1980)
review. One recent development is a refined error analysis of the
Be - log re relation
(Boroson and Kormendy
1982).
This is motivated by the fact
that Be and re are coupled, a point
emphasized by
Schechter (1981).
The reason for the coupling is again that E-galaxy profiles are nearly
power laws. Boroson and Kormendy have derived
" 2 ellipses", which
represent constant root-mean-square deviations of r1/4
laws fitted to the profiles. The
2 ellipses", which
represent constant root-mean-square deviations of r1/4
laws fitted to the profiles. The
 2 ellipses in the
Be - log re plane are very
elongated and have a slope of ~ 5. That is, the coupling tends to
preserve MB. A few of the largest
2 ellipses in the
Be - log re plane are very
elongated and have a slope of ~ 5. That is, the coupling tends to
preserve MB. A few of the largest
 2 ellipses have
lengths which are nearly one-quarter of the parameter range seen in
Figure 13. However,
most are much smaller than this. It is clear that the parameter
coupling has only a small effect on the Be - log
re relation.
2 ellipses have
lengths which are nearly one-quarter of the parameter range seen in
Figure 13. However,
most are much smaller than this. It is clear that the parameter
coupling has only a small effect on the Be - log
re relation.
However, if the fits are allowed to be, less precise, then the
 2
ellipses grow very rapidly. Thus large fitting errors tend to scatter
the points in the Be - log re
diagram along a line of slope ~ 5 (the
slope of the
2
ellipses grow very rapidly. Thus large fitting errors tend to scatter
the points in the Be - log re
diagram along a line of slope ~ 5 (the
slope of the  2
ellipses). This may account for the fact that
Strom and Strom (1978a,
b,
c)
observe slopes between 3.3 and 5: they fit
r1/4 laws between an inner radius limit and an outer
brightness limit, even in tidally distended or truncated galaxies
(section 3.3.5),
without examining the quality of the fits.
2
ellipses). This may account for the fact that
Strom and Strom (1978a,
b,
c)
observe slopes between 3.3 and 5: they fit
r1/4 laws between an inner radius limit and an outer
brightness limit, even in tidally distended or truncated galaxies
(section 3.3.5),
without examining the quality of the fits.