5.1.5. Dynamics of Bars.
The Importance of Rotation Versus Random Motions: Comparison with N-Body Models

In this section I examine the radial variation in NGC 936 and in the n-body models of the ratio V / of rotation velocity to velocity dispersion. As discussed in section 4.2.6, V / measures the relative dynamical importance of ordered and random motions.

In the following discussion all radii are scaled to a common dimensionless system by dividing them by the corotation radius r_cor. This is a natural length scale because theoretical arguments suggest that bars end at or just inside corotation (e.g., Contopoulos 1979, 1980; Sellwood 1980, 1981). Values of r_cor are given in MS and in HZ. For NGC 936 I assume that r_cor = r_B = 51" along the major axis. The probable sense of any error in this assumption is that r_cor may be larger than the adopted value.

Figure 45 shows the radial dependence of V / in NGC 936 and in the models. Since kinematic data for the projected MS model are given for only two orientations, I use these in the left-hand panel for a comparison with the HZ model. In both cases the bar is edge-on, and the "spectrograph slit" is in the equatorial plane. V / is slightly larger when the bar is seen end-on than when it is viewed broadside. However, the two models behave very similarly from the center to-a radius r / r_cor ~ 0.7. Here the difference in initial velocity dispersions may begin to have a significant effect (Zang 1981). To investigate the importance of projection, the left panel also shows unprojected but azimuthally averaged V / values for the equatorial plane of the HZ model. These are very well approximated by the average of the curves for the bar seen broadside and end-on. Projection effects on V / are not large.

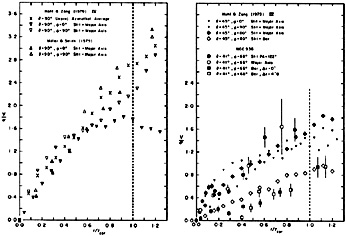Figure 45. The local ratio of velocity to velocity dispersion for n-body bar models and for NGC 936. All quantities except the crosses refer to projected configurations. Radii r are normalized to the corotation radius rcor. The viewing geometry is given in the notation of Hohl and Zang (1979): = 90° - i, i the inclination, is equal to 90° when the model is edge-on. The angle in the disk plane between the bar and the kinematic major axis is called here and ' in the text. When = 0°, the bar is perpendicular to the line of sight. In the right-hand panel, the large symbols for the model are directly comparable with the observations.

In the right-hand panel of Figure 45, the inclination of the HZ model is approximately equal to that of the galaxy. Rotation is considerably reduced at i = 45° or 49°. The dispersion is changed less, because the model bar is as thick as it is wide. Two sets of points are shown in the figure, corresponding to measurements of NGC 936 made along the major axis and bar. When the slit is placed along the kinematic major axis of the model, the values of V / obtained are insensitive to the orientation of the bar (upper set of points). Those NGC 936 measurements which refer to the bar (0.2 r / r_cor 1) are consistent with the points for the HZ model. (At smaller radii the points for NGC 936 show a peak in V / which refers to the rapidly-rotating bulge.) If the slit is placed along the bar rather than the major axis, the velocities decrease by a factor of ~ 2, while changes little. Again the behavior of the model is similar to that of the galaxy, although NGC 936 appears to be slightly hotter than the model. This difference is decreased if the real corotation radius is larger than the assumed value.

There are two possible problems with the above discussion. First, the model bar is probably less flattened than the real one. When the model is seen at i = 45°, V / is therefore smaller than it should be because of the large axial velocity dispersion. Therefore, Figure 45 slightly underestimates the amount that the galaxy is hotter than the model. The second potential problem is the behavior of the Fourier velocity program when presented with spectra of a mixture of populations with different dispersions (section 4.2.1; Fig. 32). Given the rather isotropic velocity dispersions illustrated in Figure 41, this is not a major worry. However, the effect should be kept in mind as we make increasingly detailed comparisons of models and observations.