3.7. Rate of Cluster Formation Evolution:

The rate of growth of perturbations is different in universes with different matter content. For example, the perturbation growth in a _m = 1 universe is proportional to the scale factor, ie., (1 + z)^-1, while in the extreme case of an empty universe (_m = 0); = constant. From (32) we see that _m < 1 universes will behave dynamically as an = 1 universe at large enough redshift, and at some redshift z ~ 1 curvature dominates and perturbations stop evolving and freeze, allowing clusters to relax up to the present epoch much more than in an _m = 1 model, in which clusters are still forming. This can be seen clearly in Fig.15 where we plot the evolution of the perturbation growth factor, defined as:

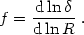
For a = 0 universe, f _m^0.6 (cf. [115]) and thus for the EdS model f = 1. For > 0 models there is a redshift dependence of f, but in the present epoch it is indistinguishable from the corresponding value of the open (_m = 1 - ) model [86]. It is evident that an 0 < < 1 universe behaves as an _m = 1 model up to a lower redshift than the corresponding open model, while at redshifts z 1 it behaves like an open model, which implies that clusters should be dynamically older in such a model than in the EdS.

Figure 15. The evolution of the perturbation growth factor, f, in 3 models (EdS, open m = 0.3 and the currently popular flat = 0.7). The vertical dashed lines indicate the redshift range 0.3 z 1 where the 3 models, jointly, differ maximally.

Therefore one should be able to put constraints on from the evolution of various indicators of cluster formation, especially in the range where the dynamical evolution between the models differs maximally (vertical dashed lines in Fig.15).

Ideally, one would like to study the evolution of the cluster mass function but since light is what we observe (temperature as well - due to the hot ICM X-ray emission), various related indicators are usually studied (Luminosity function, temperature function, morphology etc), but then one has to pass through the machinery provided by the Press-Schechter formalism [128], which gives the mass function of collapsed halos at any epoch as a function of the cosmological parameters that enter through the assumed power spectrum of perturbations.

Luminosity function: Based mostly on EINSTEIN and ROSAT surveys, many studies have found an evolving X-ray luminosity function, ie., less z 0.3 clusters than expected for a no-evolving luminosity function, ie., a negative evolution (cf. [63] and references therein). Such a behaviour is expected in models with

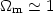
However, see [69] for a different view.

Temperature function: Estimates of the temperature of the X-ray emitting ICM gas can be reliably estimated from the iron line-emission. Then the cluster temperature can be either transformed to a mass (assuming hydrostatic equilibrium and isothermality) and thus derive a mass function to compare with the Press-Schechter predictions (cf. [133] and references therein) pointing to _m < 0.3 , or use the evolution of the temperature distribution function. Again different studies find either no evolution (cf. [56], [68]) pointing to

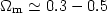
or evidence for evolution [180], [19] pointing to

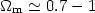
Evolution of L - T relation: Under the assumption of hydrostatic equilibrium and isothermality one can easily show, from Euler's equation, that the bremsstrahlung radiation temperature is T M_v / R_v (where M_v and R_v are the cluster virial mass and radius). Using the spherical collapse top-hat model [114] one obtains R_v T^1/2 (z)^-1/2 E(z)^-1/2, and then by using (56):

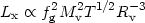
(92)

where f_g is the gas mass fraction. Then one finds (cf. [31]):

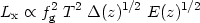
where E(z) is given by (18) and (z) is the ratio of the average density within the virialized cluster ( R_v) and the critical density at redshift z, which also depends on the cosmological model. However, this model fails to account for observations which show a steeper T-dependence, L_x T ^3-3.3 (such a dependence can be recovered from (92) if f_g T^1/2). In any case, the L - T relation is expected to evolve with time in a model dependent way. Most studies (see references in [155]) have found no evolution of the relation while a recent study of a deep (z ~ 0.85) ROSAT cluster survey [25] found:

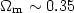
However, there are many physical mechanisms that affect this relation (eg. gas cooling, supernova feedback etc) and in ways which are not fully understood (cf. [66]).

Evolution of Cluster Morphology: As we have already discussed, in an open or a flat with vacuum-energy contribution universe it is expected that clusters should appear more relaxed with weak or no indications of substructure. Instead, in a critical density model, such systems continue to form even today and should appear to be dynamically active (cf. [134], [59], [85]). Using the above theoretical expectations as a cosmological tool is hampered by two facts (a) Ambiguity in identifying cluster substructure (due to projection effects) and (b) Post-merging relaxation time uncertainty (cf. [150]). However, criteria of recent merging could be used to identify the rate of cluster morphology evolution and thus put constraints on _m. Such criteria have been born out of numerical simulations (cf. [139], [140]) and are based on the use of multiwavelength data, especially optical and X-ray data but radio as well (cf. [192], [154]). The criteria are based on the fact that gas is collisional while galaxies are not and therefore during the merger of two clumps, containing galaxies and gas, we expect: (1) a difference in the spatial positions of the highest peak in the galaxy and gas distribution, (2) due to compression, the X-ray emitting gas to be elongated perpendicularly to the merging direction, and (3) temperature gradients to develop due to the compression and subsequent shock heating of the gas. The first two indicators are expected to decay within ~ 1 Gyr after the merger, while the last may survive for a considerably longer period (see for example Fig.16).

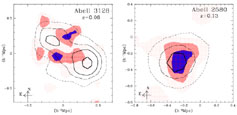
Figure 16. Optical APM (colour) and ROSAT X-ray (contour) images of 2 ABELL clusters. Peaks of the APM galaxy distribution is shown in blue. A3128 has the signature of a recent merger: the peaks in the distribution of galaxies and in X-ray emitting gas are orthogonal to each other. A2580 on the other side seems a smooth relaxed cluster with the gas and galaxies tracing the cluster potential (from [120]).

However, a rather cruder but still useful test of cluster morphological evolution could be used. For example, cluster ellipticity is a relatively well defined quantity; although systematic effects due to projections in the optical or the strong central concentration of the X-ray emitting gas (since L_x n_e²), should be taken into account (cf. [81]). An early study, using the Lick map [121], had found that cluster ellipticity decreases with redshift, however due to possible systematic effects involved in the construction of the data, they did not attach any weight to this discovery. Recently, two studies using optical and/or X-ray data [100], [127] (see also [120]) found that indeed the cluster ellipticity decreases with redshift in the recent past, z 0.15 (see Fig.17) This was interpreted by [100] as an indication of a low-_m universe because in such a universe one expects that merging and anisotropic accretion of matter along filaments will have stopped long ago. Thus the clusters should be relatively isolated and gravitational relaxation will tend to isotropize the clusters reducing their ellipticity, more so in the recent times.

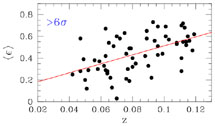
Figure 17. The evolution of ellipticity in APM clusters with significant substructure [120].

If this is the case then one should expect an evolution of the temperature of the X-ray emitting gas as well as the X-ray cluster luminosity which should follow the same trend as the cluster ellipticity, decreasing at recent times, since the violent merging events, at relatively higher redshifts, will compress and shock heat the diffuse ICM gas [138]. Such evidence was presented in [127] using a compilation of measured ICM temperatures and luminosities in two volume limited X-ray cluster samples (based on the XBAC and BCS samples). Also, one could naively expect an evolution of the cluster velocity dispersion, increasing at lower redshifts, since virialization will tend to increase the cluster ‘thermal' velocity dispersion. In [65] no evolution was found between a local sample (z 0.15) and a distant one 0.15 z 0.9. However, unrelaxed clusters can also show up as having a high velocity dispersion due to either possible large peculiar velocities of the different sub-clumps [142] or due to the possible sub-clump virialized nature. Therefore, a better physical understanding of the merging history of clusters is necessary in order to be able to utilize the velocity dispersion measure as an evolution criterion.

Other related studies, using the morphological characteristics of the large-scale structures, have been used to place cosmological constraints. For example, the shapes of superclusters and voids, using the IRAS-PSCZ redshift survey and the ABELL/ACO cluster distribution show a clear preference for a -CDM model over a _m = 1 model [13], [126], [82], [102] but see [2].