7.1. A Decaying Cosmological Constant?

One method of resolving the dilemma between a very large cosmological constant (predicted by field theory) and an extremely small one (suggested by observations) with obvious cosmological advantages is to make the cosmological term time-dependent. An initially large cosmological term would give rise to Inflation, ameliorating the horizon and flatness problems and (possibly) seeding galaxy formation. The subsequent slow decay of (t) would enable a small present value (t₀) to be reconciled with observations suggesting ~ 0.7. (A time dependent cosmological term of course arises in Inflationary models and during cosmological phase transitions, but in such cases the post-inflationary decay of the cosmological term is very rapid.)

The first proposal for dynamically reducing the cosmological constant was made by Dolgov (1983) who considered a massless non-minimally coupled scalar field having the Lagrangian density

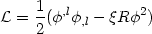
(74)

and the resulting equation of motion

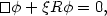
(75)

where R is the scalar curvature and the coupling to gravity. Considering the special case of a homogeneous scalar field, the Einstein equations become

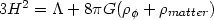
(76)

where

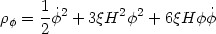
(77)

is the scalar field energy density. The scalar field equation (75) reduces to

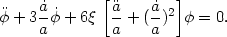
(78)

Dolgov made the discovery that, for negative values of , the scalar field is unstable: its energy density becomes large and negative compensating for the cosmological constant in (76), so that the resulting effective cosmological constant rapidly decays to zero. Let us demonstrate this by examining the Einstein equation (76) which together with the scalar field equation (78) defines a pair of nonlinear differential equations determining the behaviour of the scale factor a(t) and the scalar field (t). The term 3 H^{2 2} in can be carried over into the left hand side of (76) resulting in

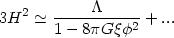
(79)

As Dolgov demonstrated, (t) grows with time if < 0, so that the effective cosmological constant _eff = /(1 + 8 G|| ²) decreases. The late time behaviour of a(t), (t) obtained by solving (76 - 78) with _m << has the asymptotic form [46, 66]

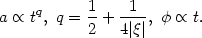
As a result, lim_{t eff} 0 i.e. the cosmological term vanishes at late times.

Unfortunately this mechanism cannot be used in real universe. The first problem with this approach is that the very mechanism which decreases the cosmological constant also quenches the effective gravitational constant, since from (76),

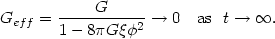
(80)

As a result, the effective gravitational constant becomes noticeably time-dependent: 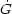_eff / G_eff = - 2/t ~ - 10^-10 yr^-1, which strongly contradicts upper limits from Viking radar ranging [87] and lunar laser ranging experiments [211]. Another problem is that such screening of is still not sufficient. The remaining part of remains of the order of the Ricci tensor all the time, while we need it to be much less than the Ricci tensor during the matter dominated epoch to obtain sufficient growth of scalar perturbations. Finally, _m << 1 during this regime.

An extension of this method to higher spin fields (massless vector and tensor) can remove the first drawback by making a cancellation of the cosmological constant possible while keeping the gravitational coupling constant time-independent [47]. However, the other difficulties (especially, the second one) remain. This shows that it is not easy to explain the observed -term by a cancellation mechanism. Still this aesthetically attactive possibility should be investigated further (some variants of the early Dolgov mechanism are discussed in [10, 205]).