3.2. Quintessential Inflation in Braneworld scenario's

In the 4+1 dimensional brane scenario inspired by the Randall-Sundrum [47] model, matter fields are confined to a three dimensional `brane' which is embedded in a four dimensional `bulk' geometry. The equation of motion of a scalar field propogating on the brane is

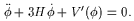
(10)

where [48]

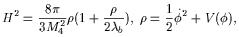
(11)

and _b is the brane tension. The additional term ² / _b in (11) arises due to junction conditions imposed at the bulk-brane boundary. The presence of this term increases the damping experienced by the scalar field as it rolls down its potential. This effect is reflected in the slow-roll parameters, which in braneworld models (for V / _b >> 1) have the form [38]

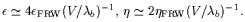
(12)

Clearly slow-roll (, << 1) is easier to achieve when V / _b >> 1 and on this basis one can expect inflation to occur even for the very steep potentials associated with quintessence models including V e , V ^- etc. Inflation in these models has been extensively discussed in [39, 40, 41, 42] within the framework of a scenario in which reheating takes place unconventionally, through inflationary particle production. This leads to an enormous difference between the energy in the inflaton and in radiation at the end of inflation: / _rad |_end ~ 10¹⁶. Since the potential driving inflation is steep, the post-inflationary expansion in these models is driven by the kinetic energy of the scalar field, so that w 1, a^-6 and a t^1/3. (Because radiation decreases at the slower rate _rad a^-4 the scale factor changes to a t^1/2 after the density in the inflaton and in radiation equalize. This usually takes place at a low temperature T_eq ~ few GeV.)

As demonstrated in [39, 40, 41, 42] inflation can occur for several of the quintessence potentials discussed in the previous section but for a rather narrow region of parameter space (see figure 2). It also appears that quintessential inflation generates a large gravity wave background which could be in conflict with big bang nucleosynthesis considerations [41].

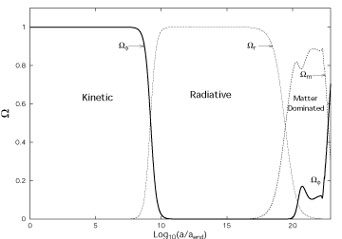
Figure 2. The post-inflationary density parameter is plotted for the scalar field (solid line) radiation (dashed line) and cold dark matter (dotted line) in the quintessential-inflationary model decribed by (9) with p = 0.2. Late time oscillations of the scalar field ensure that the mean equation of state turns negative <w> - 2/3, giving rise to the current epoch of cosmic acceleration with a(t) t2 and present day values 0 0.7, 0m 0.3. From Sahni, Sami and Souradeep [41].