The conventional viewpoint regarding the future evolution of a matter-dominated universe can be summarised by the following pair of statements:
[A] If the universe is spatially open or flat then it will expand for ever.
[B] Alternatively, if the universe is spatially closed then its expansion will be followed by recollapse.
In a 
-dominated
universe [A] and [B] are replaced by
[A'] A spatially open or flat universe
(
= 0, -1)
will recollapse if the
-term is
constant and negative.
[B'] A closed universe
( = +1)
with a constant positive
-term can,
under certain circumstances, expand forever.
Recent CMB observations indicate that our universe is close to
being spatially flat, therefore, if we wait long enough we will find that
the expansion of our universe rapidly approaches the
de Sitter value H =
H
= [/3]1/2
= H0[1 -
m]1/2, while
the density of matter asymptotically declines to zero
m
a-3
0.
Density perturbations in such a universe will freeze to a constant value
if they are still in the linear regime,
but the acceleration of
the universe will not affect gravitationally bound systems on present scales
of R < 10h-1 Mpc (which includes our own galaxy as
well as galaxy clusters).
The universe at late times will therefore consist of islands of matter
immersed in an accelerating sea of dark energy:
`'.
In such a universe the local neighborhood of an observer from which he/she is able to receive signals will eventually contract and shrink so that even those regions of the universe which are currently observable to us will eventually be hidden from view. As an illustration consider an event at (r1, t1) which we wish to observe at our location at r = 0, then
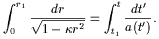
| (19) |
An observer at r = 0 will be able to receive signals from any event
(after a suitably long wait) provided
the integral in the RHS of (19) diverges (as
t
).
For a
t p,
this implies p < 0, or a decelerating universe.
In an accelerating universe the integral converges, signaling the presence
of an event horizon.
As a result one can only receive signals from those events which satisfy
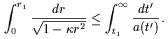
| (20) |
For de Sitter-like expansion
a = a1
expH(t-t1), H =
[/3]1/2,
we get r1 
rH and
R = a1rH = H-1
where R is the proper distance to the event horizon.
In such a universe light emitted by distant objects gets redshifted and
declines in intensity
(an analogous situation occurs for an object falling through the
horizon of a black hole.) As a result
comoving observers once visible, gradually disappear
from view as the universe accelerates under the influence of
.
One consequence of this interesting phenomenon is that
at any given instant of time, t0, one can
determine a redshift zH, which will define for us
the `sphere of influence' of our civilization.
Celestial objects with z > zH will always remain
inaccessible to signals emitted by our civilization at
t 
t0.
For a
-dominated
universe with
m = 0.3,
= 0.7 one finds
zH = 1.80
[21].
More generally,
horizon's exist in a universe which begins to perpetually accelerate
after a given point of time
[54,
55].
(To this general category belong models of dark energy
with equation of state -1 < w < - 1/3, as well as `runaway
scalar fields'
[56]
which satisfy V, V', V"
0 and
V'/V, V"/V
0 as
.)
Since the conventional S-matrix approach may not work in a universe with an
event horizon, such a cosmological model
may pose a serious challenge to a fundamental theory of
interactions such as string theory.
Possible ways of cutting short `eternal acceleration' (thereby
avoiding horizons) involve scalar fields with non-monotonic potentials.
For instance a flat potential with a local minimum
will have a negative equation of state during slow roll,
which will increase to non-negative values after the cessation of
slow roll and the commencement of oscillations (provided the potential
is sufficiently steep in the neighborhood of the minimum).
An example is provided by a massive scalar field
V() =
m2
2/2
for which the epoch of accelerated expansion is a transient.
Other possibilities are discussed in
[55,
57,
43,
44,
58,
59].