2.3. The naive estimator

From the definition of a probability density, if the random variable X has density f, then

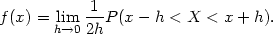
For any given h, we can of course estimate P(x - h < X < x + h) by the proportion of the sample falling in the interval (x - h, x + h). Thus a natural estimator of the density is given by choosing a small number h and setting

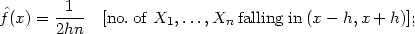
we shall call this the naive estimator.

To express the estimator more transparently, define the weight function w by

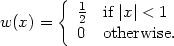
(2.1)

Then it is easy to see that the naive estimator can be written

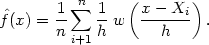
It follows from (2.1) that the estimate is constructed by placing a `box' of width 2h and height (2n h)^-1 on each observation and then summing to obtain the estimate. We shall return to this interpretation below, but it is instructive first to consider a connection with histograms.

Consider the histogram constructed from the data using bins of width 2h. Assume that no observations lie exactly at the edge of a bin. If x happens to be at the centre of one of the histogram bins, it follows at once from (2.1) that the naive estimate (x) will be exactly the ordinate of the histogram at x. Thus the naive estimate can be seen to be an attempt to construct a histogram where every point is the centre of a sampling interval, thus freeing the histogram from a particular choice of bin positions. The choice of bin width still remains and is governed by the parameter h, which controls the amount by which the data are smoothed to produce the estimate.

The naive estimator is not wholly satisfactory from the point of view of using density estimates for presentation. It follows from the definition that is not a continuous function, but has jumps at the points X_i ± h and has zero derivative everywhere else. This gives the estimates a somewhat ragged character which is not only aesthetically undesirable, but, more seriously, could provide the untrained observer with a misleading impression. Partly to overcome this difficulty, and partly for other technical reasons given later, it is of interest to consider the generalization of the naive estimator given in the following section.

A density estimated using the naive estimator is given in Fig. 2.3. The `stepwise' nature of the estimate is clear. The boxes used to construct the estimate have the same width as the histogram bins in Fig. 2.1.

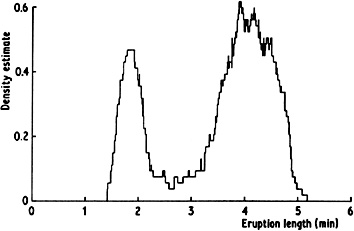
Fig. 2.3 Naive estimate constructed from Old Faithful geyser data, h = 0.25.