2. BASICS OF ABUNDANCE DETERMINATIONS IN IONIZED NEBULAE

2.1. Empirical methods

These are methods in which no check is made for the consistency of the derived abundances with the observed properties of the nebulae. They can be schematically subdivided into direct methods and statistical methods.

2.1.1. Direct methods

The abundance ratio of two ions is obtained from the observed intensity ratio of lines emitted by these ions. For example, O⁺⁺/H⁺ can be derived from

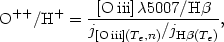(1.27)

where j_{[O III]}(T_e, n) is the emission coefficient of the [O III] 5007 line, which is dependent on T_e and n (assumed uniform in the nebula).

T_e can be derived using the ratio of the two lines [O III] 4363 and [O III] 5007, which have very different excitation potentials. Other line ratios can also be used as temperature indicators in nebulae, such as [N II] 5755/6584 and [S III] 6312/9532. The Balmer and Paschen jumps, the radio continuum and radio recombination lines also allow to estimate the electron temperature, but the measurements are more difficult.

The density is usually derived from intensity ratios of two lines of the same ion which have the same excitation energy but different collisional deexcitation rates. The most common such ratio is [S II] 6731/6717. Far infrared lines can also be used to determine densities. Each line pair is sensitive in a given density range (about 2 to 3 decades), which can be ranked as follows (Rubin et al. 1994): [NII] 122µ / 205µ, [OIII] 52µ / 88µ, [SII] 6731/6717, [OII] 3726/3729, [SIII] 18.7µ / 33.6µ, [AIV] 4740/4711, [NeIII] 15.5µ / 36.0µ, [AIII] 8.99µ / 21.8µ, CIII] 1909/1907. The electron density can also be measured by the ratio of high order hydrogen recombination lines.

Plasma diagnostic diagrams combining all the information from temperature- and density-sensitive line ratios can also be constructed for a given nebula (e.g. Aller & Czyzak 1983), plotting for each pair of diagnostic lines the curve in the (T_e, n) plane that corresponds to the observed value. The curves usually do not intersect in one point, due to measurement errors and to the fact that the nebula is not homogeneous (and also to possible uncertainties in the atomic data) and provide a visual estimate of the uncertainty in the adopted values of T_e and n.

The total abundance of a given element relative to hydrogen is given by the sum of abundances of all its ions. In practise, not all the ions present in a nebula are generally observed. The only favourable case is that of oxygen which in H II regions is readily determined from:

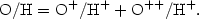(1.28)

Note that even if [O I] 6300 is observed, it should not be included in the determination of the oxygen abundance, since the reference hydrogen line is emitted by H⁺, while O⁰ is tied to H⁰.

In almost all other cases (except in some cases when multiwavelength data are available), one must correct for unseen ions using ionization correction factors. A common way to do this in the 70' and 80' and even later was to rely on ionization potential considerations, which led to such simple expressions as:

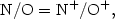	(1.29)
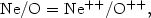	(1.30)
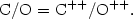	(1.31)

In high excitation PNe where He II lines are seen, oxygen can be present in ionization stages higher than O⁺⁺. A popular ionization correction scheme for oxygen (e.g. Torres-Peimbert & Peimbert 1977) was:

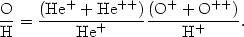(1.32)

Expressions (2.29 - 2.31) are based on the similarity the ionization potentials of C⁺, N⁺, O⁺, Ne⁺. Expression (2.32) is based on the fact that the ionization potentials of He⁺ and O⁺⁺ are identical.

However, photoionization models show that such simple relations do not necessarily hold. For example, the charge transfer reaction O⁺⁺ + H⁰ O⁺ + H⁺ being much more efficient than the Ne⁺⁺ + H⁰ Ne⁺ + H⁺ one, Ne⁺⁺ is more recombined than O⁺⁺ in the outer parts of nebulae and in zones of low ionization parameter.

Also, while it is true that no O⁺⁺⁺ ions can be found outside the He⁺⁺ Strömgren sphere, since the photons able to ionize O⁺⁺ are absorbed by He⁺, O⁺⁺ ions can well be present inside the He⁺⁺ zone.

Ionization correction factors based on grids of photoionization models of nebulae are therefore more reliable. Complete sets of ionization correction factors have been published by Mathis & Rosa (1991) for H II regions and Kingsburgh & Barlow (1994) for planetary nebulae, or can be computed from grid of photoionization models such as those of Stasinska (1990), Gruenwald & Viegas (1992) for single star H II regions, Stasinska et al. (2001) for giant H II regions, Stasinska et al. (1998) for PNe.

However, it must be kept in mind that ionization correction factors from model grids may be risky too, both because the atomic physics is not well known yet (see Sect. 3.1) and because the density structure of real nebulae is more complicated than that of idealized models. The most robust relation seems to be N/O = N⁺ / O⁺ (but see Stasinska & Schaerer 1997). Such a circumstance is fortunate, given the importance of the N/O ratio both in H II regions (as a constraint for chemical evolution studies) and in PNe (as a clue on PNe progenitors).

In spite of uncertainties, ionization correction factors often provide more accurate abundances than summing up ionic abundances obtained combining different techniques in the optical, ultraviolet and infrared domains.

Note that there is no robust empirical way to correct for neutral helium to derive the total helium abundance. The reason is that the relative populations of helium and hydrogen ions mostly depend on the energy distribution of the ionizing radiation field, while those of ions from heavy elements are also a function of the gas density distribution.

In summary, direct methods for abundance determinations are simple, powerful, and provide reasonable results (provided one keeps in mind the uncertainties involved, which will be developed in the next sections). Until recently, abundances were mostly derived from collisionally excited optical lines. This is still the case, but the importance of infrared data is growing, especially since the ISO mission. IR line intensities have the advantage of being almost independent of temperature. They arise from a larger variety of ions than optical lines. They allow to probe regions highly obscured by dust. However, they suffer from beamsize and calibration problems which are far more difficult to overcome than in the case of optical spectra. Abundance determinations using recombination lines of heavy elements have regained interest these last years. They require high signal-to-noise spectroscopy since the strengths of recombination lines from heavy elements are typically 0.1% of those of hydrogen Balmer lines. They will be discussed more thoroughly in the next sections, since they unexpectedly pose one of the major problems in nebular astrophysics.