3.3. Reddening correction

The usual dereddening procedure is to derive the logarithmic extinction at H, C, from the observed H / H ratio, assuming that the intrinsic one has the value (H / H)_B predicted by case B recombination:

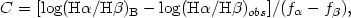(3.33)

where f and f represent the values of the reddening law at the wavelengths of the H and H lines respectively.

Then, for any observed line ratio (F₁ / F₂)_obs one can obtain the reddening corrected value (F₁ / F₂)_corr from:

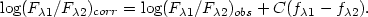(3.34)

Ideally, one can iterate after having determined the electron temperature of the plasma, to use a value of (H / H)_B at the appropriate temperature.

There are nevertheless several problems. One is that the extinction law is not universal. As shown by Cardelli et al. (1989), it depends on the parameter R_V = A_V / E(B - V), where A_V is the absolute extinction in V and E(B - V) is the color excess. While the canonical value of R_V is 3 - 3.2, the actual values range from 2.5 to 5 (Cardelli et al. 1989, Barbaro et al. 2001, Patriarchi et al. 2001). Objects located in the Galactic bulge suffer from an extinction characterized by a low value of R_V (e.g. Stasinska et al. 1992, Liu et al. 2001). Cardelli et. el. (1989) attribute these differences in extinction laws between small and large values of R_V to the presence of systematically larger particles in dense regions. These variations in R_V have a significant effect on line ratios when dealing with ultraviolet spectra. It is therefore convenient to link the optical and ultraviolet spectra by using line ratios with known intrinsic value, such as He II 1640 / He II 4686.

Another difficulty is that dust is not necessarily entirely located between the object and the observer as in the case of stars. Some extinction may be due to dust mixed with the emitting gas. In that case, the wavelength dependence of the extinction is different and strongly geometry dependent (Mathis 1983). One way to proceed, which alleviates this problem, is to use the entire set of observed hydrogen lines and fit their ratios to the theoretical value, which then gives an empirical reddening law to deredden the other emission lines. This, however, is still not perfect, since the extinction suffered by lines emitted only at the periphery of the nebula, or, on the contrary, only in the central parts, is different from the extinction suffered by hydrogen lines which are emitted in the entire nebular body. The problem is further complicated by scattering effects (see e. g. Henney 1998).

In the case of giant H II regions, where the observing slit encompasses stellar light, one must first correct for the stellar absorption in the hydrogen lines. This can be done in an iterative procedure, as outlined for example by Izotov et al. (1994).

A further problem is that the intrinsic hydrogen line ratios may deviate from case B theory. This occurs for example in nebulae with high electron temperature (~ 20000 K), where collisional contribution to the emissivity of the lowest order Balmer lines may become significant. In that case, a line ratio corrected assuming case B for the hydrogen lines, (F₁ / F₂)_B is related to the true line ratio (F₁ / F₂)_true by:

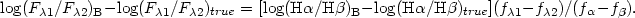(3.35)

The error is independent of the real extinction and can be large for 1 very different from 2. For example, it can easily reach a factor 1.5 - 2 for C III] 1909 / [O III] 5007 (see Stasinska 2002).

Whatever dereddening procedure is adopted, it is good practise to check whether the H / H value has the expected value. If not, the [O III] 4363/5007 ratio will be in error by a similar amount.