3.5.2. Small scale temperature variations

If the temperature in a nebula is not uniform, T_e-based empirical abundances are biased. Peimbert (1967) developed a mathematical formulation to evaluate the bias. It is based on the Taylor expansion of the average temperature

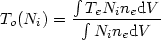(3.36)

defined for each ion N_i, using the r.m.s. temperature fluctuation

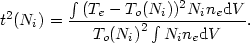(3.37)

From comparison of temperatures measured by different methods, this temperature fluctuation scheme led to conclude that temperature fluctuations are common in nebulae, with typical values of t² = 0.03 - 0.05 (see references in Peimbert 1996, Stasinska 1998, Mathis et al. 1998, Esteban 2002). The case is not always easy to make: the determination of the continuum in the vicinity of the Balmer jump is difficult, the combination of data from different instruments for the comparison of far infrared data with optical ones involves many potential sources of errors, lines of O⁺⁺ and of H are not emitted in coextensive zones etc ... Nevertheless, the observational results seem overwhelming. And, as noted by Peimbert (2002), the value of t² found in such a way is never negative!

Note that in the PNe NGC 6153, NGC 7009, M1-42 and M2-36, (Liu et al. 1995, 2000, 2001, Luo et al. 2001) much larger values of t², of the order of 0.1, would be derived from the comparison of optical recombination lines (ORL) to collisionally excited lines (CEL). But this may be another problem (see Sect. 3.6).

A value of t² ~ 0.04, in the scheme of Peimbert (1967), typically leads to an underestimation of O/H by about 0.3 dex ⁽²⁾. It is thus extremely important to determine whether temperature fluctuations exist or whether they are an artefact of the techniques employed. And, if they really exist, to understand their nature and possibly derive some systematics to account for them in abundance derivations. Note that, so far, the evidences are always indirect, based on the comparison of different methods to estimate T_e. Only mapping the nebulae with appropriate sensitivity and spatial resolution in the temperature diagnostic lines could give direct evidence of small scale fluctuations. In the planetary nebula NGC 6543, HST mapping of [O III] 4363/5007 shows much smaller spatial temperature variations than expected for this object from indirect measurements (Lame et al. 1998). In NGC 4361, long slit spectroscopy gives a surface temperature fluctuation t²_s ~ 0.002 (Liu 1998). In Orion, long slit mapping of the Balmer decrement gives t²_s ~ 0.001 (Liu et al. 1995a). All these observed t²_s translate into volume temperature fluctuations t² 0.01.

Actually, the value of t² defined by Eq. (3.37) is not strictly speaking equal to the value of t² derived observationally, for example from the comparison of temperatures derived from [O III] 4363/5007 and from the Balmer jump. Kingdon & Ferland (1995) introduced the notation t²_str for the former (str meaning "structural") and t²_obs for the latter. Photoionization models of planetary nebulae and H II regions generally fail to produce such large values of t²_obs as observed in real nebulae (e.g. Kingdon & Ferland 1995, Pérez 1997), except in the case of high metallicities, i.e. equal to the canonical "solar" value or larger. Note that in this case, what produces t²_obs in the model is actually the temperature gradient discussed above. Density fluctuations could be a source of temperature fluctuations, due to increased collisional deexcitation in zones of higher density, but photoionization models including such density fluctuations also fail to return large enough values of t² (Kingdon & Ferland 1995). Note that introducing a density condensation shifts the dominant oxygen ion to a less charged one, and consequently the increase in t²(O⁺⁺) is not as important as might have been thought a priori. Viegas & Clegg (1994) argued that very high density clumps (n > 10⁵ cm^-3) could mimic the effects of temperature fluctuations by collisionally deexciting the [O III] 5007 line. The existence of such clumps is however not confirmed by the densities derived from [Ar IV] 4740/4711, from the ratio of fine structure [O III] lines and from high order Balmer decrement lines (Liu et al. 2000, 2001). Note that, if they existed, such clumps should be located very close to the star in order to emit significantly in [O III] 5007 with respect to the rest of the nebula.

As will be discussed in Sect. 3.6, abundance inhomogeneities have been proposed to solve the ORL / CEL problem (Torres-Peimbert et al. 1990, Péquignot et al. 2002). Carbon and/or oxygen rich pockets would produce zones of lower temperature (due to increased cooling). In PNe the existence of carbon rich pockets is attested from direct observations in at least a few objects (e.g. Abell 30 and Abell 78, Jacoby & Ford 1983) and these carbon rich inclusions are thought to be material coming from the third dredge up in the progenitor star (Iben et al. 1983). But the existence of oxygen rich pockets in PNe is more difficult to understand from the present day evolution models for intermediate mass stars (see Sect. 5). On the other hand, in H ii regions, especially in giant H II regions, oxygen rich pockets could be made of material ejected by Type II supernovae and not yet mixed with the gas (Elmegreen 1998).

Other origins of temperature fluctuations have also been proposed, involving additional heating processes. The fact that several detailed photoionization studies of planetary nebulae (Peña et al. 1998) or giant H II regions (García-Vargas et al. 1997, Stasinska & Schaerer 1999, Luridiana, et al. 1999, Luridiana & Peimbert 2001, Relaño et al. 2002) predict significantly lower [O III] 4363/5007 ratios than observed indeed argues for additional heating. Shock heating or conductive heating are among the possibilities to investigate. Heat conduction from hot bubbles has been examined by Maciejewski et al. (1996) and shown to be insufficient to explain the t² derived from observations. The energy requirements to produce the observed values of t² have been evaluated by Binette et al. (2001) in the hypothesis of hot spots caused by an unknown heating process. In H II regions, the mechanical energy associated with the ionizing sources (stellar winds, supernova explosions) does not seem sufficient to produce the required value of t² (Binette et al. 2001, Luridiana et al. 2001). In planetary nebulae, a considerable amount of kinetic energy is available from the central star winds. The radiative hydrodynamical models of Perinotto et al. (1998) present a temperature spike at the external shock front. This temperature increase, located in a relatively narrow external zone, is not expected to produce a higher [O III] 4363/5007 temperature than derived from the Balmer jump. In the radiative hydrodynamical models computed by Mellema & Frank (1995) for aspherical nebulae, there are areas of lower density in which cooling is inefficient and the temperature is higher due to shock heating. Mellema & Frank suggest that this may explain the differences in temperatures derived from different methods. However, a quantitative analysis remains to be done in order to check whether the predicted effect indeed reproduces what is observed. Simulations taking into account the evolution of the velocity and mass-loss rate of the fast central star wind (Dwarkadas & Balick 1998) lead to considerably more structure on smaller scales, which could be even more favorable to solve the temperature fluctuation problem. In a slightly different context, Hyung et al. (2001) have tried to explain the high temperature observed in the inner halo of NGC 6543, (15000 K as opposed to 8500 K for the bright core) by means of a simulation using a hydrodynamic code coupled to a photoionization calculation. These authors showed that mass loss and velocity variations in the AGB wind can simultaneously explain the existence of shells in the halo and the higher O⁺⁺ temperature.

Recently, Stasinska & Szczerba (2001) proposed a completely different origin for temperature fluctuations, related to photoelectric heating by dust grains. This hypothesis is also very promising and can be checked observationally (see Sect 3.7.5).

Although the t² scheme has proved very useful to uncover the possibile existence of temperature inhomogeneities, it may not be appropriate to describe the real situation. In the case where abundance inhomogeneities are the source of the temperature variations the Peimbert (1967) description is obviously inadequate. But it can also be inappropriate for nebulae of homogeneous chemical composition, as shown on a simple two-component toy model. Consider two homogeneous zones of volumes V₁ and V₂ with temperatures T₁ and T₂, electron densities n₁ and n₂, and densities of the emitting ions (e.g. O⁺⁺) N₁ and N₂. Calling f the ratio (N₂n₂V₂) / (N₁n₁V₁) of the weigths of the emitting regions, the mean electron temperature defined by Peimbert (1967) can be expressed as:

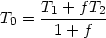(3.38)

and t² as:

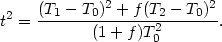(3.39)

For T₀ = 10000 K, the case f = 1 (i.e. regions of equal weight) corresponds to T₁ = 12000 K and T₂ = 8000 K. It must be realized that this 4000 K difference in temperatures requires a difference of a factor 3 in the heating or cooling rates between the two zones. When f >> 1, there is a high weight zone at T₂ T₀ and a low weight zone at T₁ >> T₀. Such a situation could correspond to a photoionized nebula with small volumes being heated by shocks or conduction. When f << 1, there is a high weight zone at T₁ T₀ and a low weight zone at T₂ << T₀ which could correspond to high metallicity clumps. With such a toy model, one can explore the biases in abundance obtained for O⁺⁺ using the [O III] 4363/5007 temperature and different lines emitted by this ion. Examples are shown in Figs. 8 and 9 of Stasinska (2002). Following expectations, O⁺⁺ derived from [O III] 5007 is generally underestimated, but it is interesting to note that the magnitude of the effect depends both on f and on T₀. The bias is very small when T₀ 15000 K. It is small in any case if f > 3 - 4, because [O III] 4363 saturates above ~ 50000K. At T₀ ~ 8000 K, O⁺⁺ is underestimated by up to a factor of 2-3 in the regime where [O III] 4363 is significantly emitted in both zones. As expected, O⁺⁺ derived from infrared fine structure lines and from the optical recombination line O II 4651 is correct. Such a toy model demonstrates that the classical temperature fluctuation scheme can be misleading. Even in a simple two zone model, the situation needs at least three parameteres to be described, not two. In our representation, these parameters would be T₁, T₂ and f, but other definitions can be used.

² N/O and Ne/O ratios are less affected by temperature fluctuations than N/H, since N/O and Ne/O abundance determinations rely on lines with similar temperature dependences and emitted in roughly the same zones. Back.