1. BULK FLOWS AS A COSMOLOGICAL PROBE

Hubble's Law, now spectacularly confirmed by the work of [27], [35], and [39], tells us that the distances of galaxies are proportional to their observed recession velocities, at least at low redshifts:

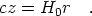
(1)

However, this is not exactly correct. Galaxies have peculiar velocities above and beyond the Hubble flow indicated by Eq. (1). We denote the peculiar velocity v(r) at every point in space; the observed redshift in the rest frame of the Local Group is then:

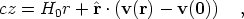
(2)

where the peculiar velocity of the Local Group itself is v(0), and 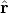is the unit vector to the galaxy in question. In practice, we will measure distances in units of km s^-1, which means that H₀ 1, and the uncertainties in the value of H₀ discussed by Freedman and Tammann in this volume are not an issue. Thus measurements of redshifts cz, and of redshift-independent distances via standard candles, yield estimates of the radial component of the velocity field. What does the resulting velocity field tell us? On scales large enough that the rms density fluctuations are small, the equations of gravitational instability can be linearized, yielding a direct proportionality between the divergence of the velocity field and the density field at late times [33], [34]:

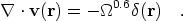
(3)

This equation is easily translated to Fourier space:

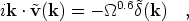
(4)

which means that if we define a velocity power spectrum P_v(k) ~ <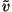²(k)> in analogy with the usual density power spectrum P(k), we find that

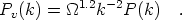
(5)

There are several immediate conclusions that we can draw from this. Peculiar velocities are tightly coupled to the matter density field (r). Therefore, peculiar velocities are a probe of the matter power spectrum; any bias of the distribution of galaxies relative to that of matter is not an issue. Moreover, Eq. (5) shows that it is in principle easier to probe large spatial scales with peculiar velocities than with the density field, because of the two extra powers of k weighting for the velocity power spectrum.

Eq. (3) shows that a comparison of the velocity field with the galaxy density field _gal allows a test of gravitational instability theory. However, in order to do this, one must assume a relation between the galaxy density field (which is observed via redshift surveys) and the mass density field (which does the gravitating). The simplest and most common assumption (other than simply assuming the two are identical) is that they are proportional (linear biasing), i.e., _gal = b. If this is the case, then we can rewrite Eq. (3) to give:

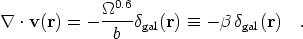
(6)

Thus if the observed density and velocity field are consistent with one another and Eq. (6), we can hope to measure . This, and other approaches to via peculiar velocities are reviewed in Dekel’s contribution to this volume; cf., the reviews by [11] and [45].