The observed distribution of galaxies from redshift surveys gives a prediction for the large-scale components of the bulk flow via the integral version of Eq. (6) . In particular, we observe from observations of the dipole anisotropy of the CMB (e.g., [24]) that the Local Group is moving with a velocity of 627 ± 22 km s-1 towards l = 276°, b = +30° (with 3° errors in each angular coordinate); this is indeed by far the most accurately measured peculiar velocity we know. One can predict this peculiar velocity from the observed galaxy distribution to be:
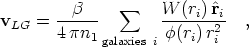
| (12) |
where 
(r) is a
selection function, to correct for the decrease in density of galaxies
as a function of distance
in a flux-limited sample, and W(r) is a window function
with cutoffs at large and small scales (cf.,
[46]).
The cutoff is needed at large distance because any flux-limited sample
has only finite depth, and
therefore the dipole one calculates is missing contributions from large
scales
([21];
[26];
[32]).
Indeed, one might think that the difference between the observed and
predicted motion of
the Local Group would be a direct measure of large-scale components of
the velocity field. Fig. 2 shows the growth of
the amplitude and direction of the predicted motion
vLG(R) as a
function of the redshift R out to which galaxies are included in
the sum, for two redshift surveys: the IRAS 1.2 Jy redshift survey
([15]; cf.,
[46]),
and the Optical Redshift Survey
([41];
[42]).
Interestingly, the two curves have a very different amplitude, which has
interesting things to
tell us about the relative bias of IRAS and optically-selected
galaxies, but discussing that
would get us too far afield. For the moment, notice that both curves
seem to converge to a
constant value (both amplitude and direction) for cz > 4000 km
s-1, implying that there is little
contribution on larger scales. This in turn would imply that the sphere
of radius 4000 km s-1 is at rest.
|
Figure 2. The amplitude (upper panel) and direction relative to the CMB dipole (lower panel) of the gravitational dipole of two surveys, the IRAS 1.2 Jy survey (solid lines) and the Optical Redshift Survey (dashed lines). Notice the apparent convergence of the dipole in both cases beyond roughly 4000 km s-1 (although the two differ quite a bit in amplitude). Notice also that the ORS is not quite as deep as the IRAS sample, and therefore the dipole calculation is cut off sooner. |
Unfortunately, things are not so simple. First, as Juszkiewicz et al. [21] pointed out, the difference between the true peculiar velocity and vLG(R) depends on the position of the center of mass of the sample out to R:
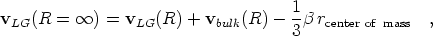
| (13) |
where vbulk (R) is the quantity we're
interested in in the current context, the mean bulk flow of the sphere
out to radius R. One can calculate the rms position of the center
of mass of a sample given a power
spectrum from linear theory; one finds another integral over the power
spectrum like Eq. (7), although with
a different smoothing kernel. This term is quite small for small values
of R, but becomes comparable
to the expected rms bulk flow for values of R above 5000 km
s-1 or so
[44],
and indeed, for
the IRAS 1.2 Jy sample, rcenter of mass is of
the order of 250 km s-1 for an outer radius of 10,000
km s-1 .
More important than this, however, are all the additional effects which
cause the quantity in Eq. (12) to
differ from the theoretical ideal. Non-linear effects, shot noise,
assuming the incorrect value of
(which of
course we don't know) and the smoothing on small scales all will
contribute to the difference between the
observed and predicted motion of the Local Group
[46].
The most pernicious effect, however, was pointed
out by [22].
With a redshift survey, one is measuring the density field in redshift
space. However, as Eq. (2) makes clear, this differs from the bulk flow
in real space by the effects of peculiar
velocities, and to the extent that the peculiar velocity field shows
coherence (which of course is
what we're trying to get a handle on here), Eq. (13) is systematically
biased. In particular,
if one's estimate of the velocity of the Local Group itself is off
(e.g., if one doesn't correct
for the v(0) term in Eq. (2) at all), the positions of all
galaxies in the sample are affected in
a dipolar way, clearly affecting the predicted motion of the Local
Group, and the apparent
convergence, or lack thereof, of
vLG(R). Strauss et al.
[46]
find that with their best correction of the
density field for peculiar velocities, the IRAS dipole indeed
seems to converge quite nicely, but
even then, there is a very intriguing, large contribution to the dipole
(albeit at the 2
level)
between 17,000 and 20,000 km s-1. It will be very
interesting to see whether this contribution
remains with the just completed PSCZ survey of IRAS galaxies to
0.6 Jy (cf., Efstathiou, this volume).