


We (Ed Ajhar, John Blakeslee, Alan Dressler, myself, and many friends) have been carrying out a survey of SBF of nearby galaxies in order to determine their distances. It has taken over five years, because we had to refigure the MDM 2.4-m optics (thanks to Paul Schechter), build CCD cameras (thanks to Gerry Luppino and Mark Metzger), and redo the computers and telescope control system (thanks to Mark Metzger) before we could carry out the northern hemisphere portion of the survey. We have used the CTIO 4-m and the LCO 2.5-m telescopes for coverage of the southern sky. We intended to finish in 1994, but we discovered that the SBF distance was more sensitive to (V - I) than we had thought and that, although we had provided overlaps between runs, the photometry from all the different runs did not knit together to satisfactory accuracy. Accordingly we spent 1995 using the MDM 1.3-m to cohect another 600 images in photometric weather, reaching far enough south that it could form a photometric backbone for the entire survey. Altogether we have collected over 5000 CCD frames, combining into more than 2000 images of 400 galaxies. Figure 6 illustrates the distribution of the SBF survey on the sky and as a function of redshift. We have more or less complete coverage of early-type galaxies with d < 2000 km s-1, substantial coverage for 2000 < d < 2800 km s-1, and some coverage of 2800 < d < 4000 km s-1. The distance errors range from 5% to 20%, with a median error of about 8%.
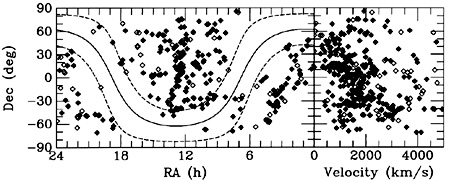 |
Figure 6. The SBF survey distributed on the sky and as a function of redshift. |
After we had completed the
 I reductions of
many galaxies, it became apparent from looking at groups that
I reductions of
many galaxies, it became apparent from looking at groups that
 I varies in a
predictable way with (V - I), that the slope seemed
to be more or less the same from group to group, and that the scatter
around the relation
was pretty much consistent with the measurement errors and the depth of
the cluster. This is illustrated in
Figure 7 for 6 groups.
I varies in a
predictable way with (V - I), that the slope seemed
to be more or less the same from group to group, and that the scatter
around the relation
was pretty much consistent with the measurement errors and the depth of
the cluster. This is illustrated in
Figure 7 for 6 groups.
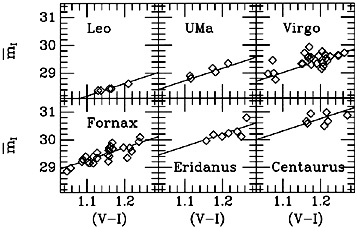 |
Figure 7. SBF measurements in six groups. |
We were led therefore to frame three hypotheses and see if they were consistent with all our data.
 I is a
1-parameter family despite the many dimensions of the contributing
stellar populations, i.e.
I is a
1-parameter family despite the many dimensions of the contributing
stellar populations, i.e.
 I has small
scatter as a function of the single parameter (V - I).
I has small
scatter as a function of the single parameter (V - I).
 I -
(V - I) slope is universal (and consistent with theory)
I -
(V - I) slope is universal (and consistent with theory)
 I -
(V - I) zero point is universal (and consistent with theory)
I -
(V - I) zero point is universal (and consistent with theory)
To this end we selected approximately 40 nearby groups of galaxies where we have more than one SBF observation. These groups are defined by position on the sky and redshift, and in most cases correspond to the groups used by the Seven Samurai. The precise list and definitions are found in TBAD96.
We can test the first two hypotheses by fitting the SBF measurement in
each galaxy  I as
I as
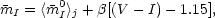 |
(3.4) |
where we fit for values of
< I0> for each of N
groups and a single value for
I0> for each of N
groups and a single value for
 . The quantity
<
. The quantity
< I0>j is the group mean value
for
I0>j is the group mean value
for  I
at a fiducial galaxy color of
(V - I) = 1.15. Our fit allows for errors in both
I
at a fiducial galaxy color of
(V - I) = 1.15. Our fit allows for errors in both
 I and (V
- I), and we also include an allowance for "cosmic
scatter" in
I and (V
- I), and we also include an allowance for "cosmic
scatter" in  I
of 0.05 mag as well as an allowance for the depth of each group which is
the rms spread across the sky divided by 21/2.
I
of 0.05 mag as well as an allowance for the depth of each group which is
the rms spread across the sky divided by 21/2.
With 149 galaxies we have 117 degrees of freedom, and we find that
 2 = 129,
2 = 129,
 2 /
N = 1.10, and the slope of the
2 /
N = 1.10, and the slope of the
 I - (V
- I) relation is 4.50 ± 0.25. The galaxies contributing
to the fit span a color range of
1.0 < (V - I) < 1.3. When we
experiment with adding
and removing different galaxies or different groups we find that the
slope changes slightly,
but is always consistent with the error above. The allowances for cosmic
scatter in
I - (V
- I) relation is 4.50 ± 0.25. The galaxies contributing
to the fit span a color range of
1.0 < (V - I) < 1.3. When we
experiment with adding
and removing different galaxies or different groups we find that the
slope changes slightly,
but is always consistent with the error above. The allowances for cosmic
scatter in  I
and group depth are poorly constrained, but if the
I
and group depth are poorly constrained, but if the
 I scatter
were increased to as much as 0.10 mag we would have to decrease the
group depth to zero to keep
I scatter
were increased to as much as 0.10 mag we would have to decrease the
group depth to zero to keep
 2 / N
equal to unity.
2 / N
equal to unity.
We therefore believe that the first two hypotheses are correct:
 I does have small
(
I does have small
( 0.05 mag) scatter
around a dependence on (V - I), and a
single slope (4.50 ± 0.25) is consistent with all of the groups.
Figure 8 illustrates how
0.05 mag) scatter
around a dependence on (V - I), and a
single slope (4.50 ± 0.25) is consistent with all of the groups.
Figure 8 illustrates how
 I depends on
(V - I)
when all the group data have been slid together by subtraction of the
group mean at (V - I) = 1.15 .
I depends on
(V - I)
when all the group data have been slid together by subtraction of the
group mean at (V - I) = 1.15 .
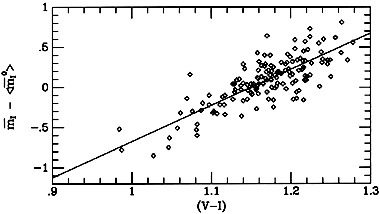 |
Figure 8. The SBF relation for all groups, brought together at (V - I) = 1.15 by the fits to group distance. The line has slope 4.5. |
We do not see any offset of spiral galaxies from early-type galaxies, so
we believe that their stellar populations are also being successfully
modeled this way. The overall rms
scatter is only 0.18 mag, and includes all the sources of scatter:
measurement error, cosmic scatter of
 I, and group
depth.
I, and group
depth.
We also find that Worthey's theoretical models give similar
results. Figure 9 shows
how  I varies as
a function of (V - I) for isochrones of age
5, 8, 12, and 17 Gyr, and
metallicity -0.50, -0.25, 0.0, +0.25, and +0.50 relative to solar. Here
we clearly see
the degeneracy of the different isochrones. The line of slope 4.5 is
consistent with these
models, and has zero point of -1.81 at (V - I) = 1.15.
I varies as
a function of (V - I) for isochrones of age
5, 8, 12, and 17 Gyr, and
metallicity -0.50, -0.25, 0.0, +0.25, and +0.50 relative to solar. Here
we clearly see
the degeneracy of the different isochrones. The line of slope 4.5 is
consistent with these
models, and has zero point of -1.81 at (V - I) = 1.15.
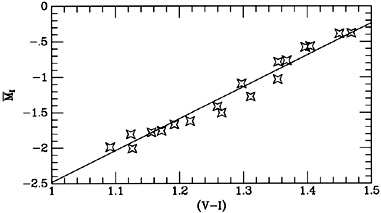 |
Figure 9. I band SBF magnitudes for various isochrones. The line has slope 4.5. |
There have been concerns about whether (V - I) is adequate to
characterize all the stellar population effects which go into
 I. In particular,
Tammann has claimed to see
a residual dependence on Mg2 after the (V - I)
dependence had been removed. In fact,
as Figure 10 illustrates, this result used an
erroneous slope of the
I. In particular,
Tammann has claimed to see
a residual dependence on Mg2 after the (V - I)
dependence had been removed. In fact,
as Figure 10 illustrates, this result used an
erroneous slope of the
 I - (V -
I) relation,
and we see no such residual dependence in Fornax or Virgo.
I - (V -
I) relation,
and we see no such residual dependence in Fornax or Virgo.
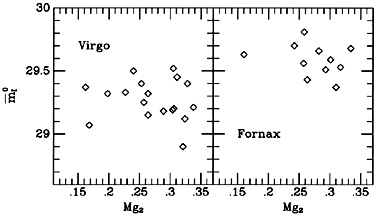 |
Figure 10. SBF, once corrected for
population differences using (V - I), shows no further
dependence on Mg2. The ordinate
|