Copyright © 1994 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1994. 32:
319-70 Copyright © 1994 by Annual Reviews. All rights reserved |
B. Sachs-Wolfe Effect
In this appendix we give a brief derivation of the Sachs-Wolfe effect in a "flat" cosmology with no cosmological constant, using the metric perturbation approach. Our starting point is the metric (following Sachs & Wolfe 1967)
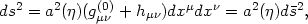
| (42) |
where a( )
is the scale factor,
)
is the scale factor,
 is the
conformal time and
gµ
is the
conformal time and
gµ (0) is
the unperturbed metric (Minkowski space). To understand the
temperature fluctuations induced by the perturbations we need to study
the photon trajectories in ds2. For photon (null)
geodesics ds2 = 0,
so by (42) there is a 1-to-1 correspondence between photon paths in
ds2 and
d
(0) is
the unperturbed metric (Minkowski space). To understand the
temperature fluctuations induced by the perturbations we need to study
the photon trajectories in ds2. For photon (null)
geodesics ds2 = 0,
so by (42) there is a 1-to-1 correspondence between photon paths in
ds2 and
d 2. This
allows us to consider the problem first in
d
2. This
allows us to consider the problem first in
d 2 and
later translate our results in ds2.
2 and
later translate our results in ds2.
We can solve for the geodesics by extremizing the Lagrangian
gµ
 µ
µ
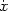
 ;
the geodesic (Euler-Lagrange) equations for
d
;
the geodesic (Euler-Lagrange) equations for
d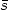 2 are
2 are
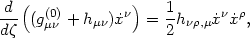
| (43) |
where  is a
parameter along the photon trajectory and the overdot
represents differentiation w.r.t.
is a
parameter along the photon trajectory and the overdot
represents differentiation w.r.t.
 . The term in
parenthesis is the
4-momentum kµ. Integrating, we find
. The term in
parenthesis is the
4-momentum kµ. Integrating, we find
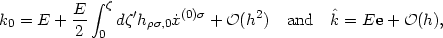
| (44) |
where E is the unperturbed energy and
x(0) = (const +
 ',
',
 'e)
is the unperturbed photon path.
'e)
is the unperturbed photon path.
The photon energy seen by an observer with 4-velocity u(|u2| = 1) is k . u. Using u = (1 - 1/2 h00, v) with |v| << 1 and (43)
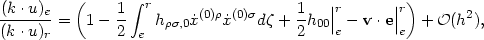
| (45) |
where e and r refer to "emission" and "reception"
respectively. The
corresponding expression in ds2 comes from multiplying
the whole expression by
a( r)
/ a(
r)
/ a( e) to account for the cosmological redshift.
e) to account for the cosmological redshift.
If we assume a uniform source and use the correspondence
h00 = 2 between the metric perturbation and the Newtonian potential the
temperature fluctuation induced is
between the metric perturbation and the Newtonian potential the
temperature fluctuation induced is
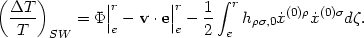
| (46) |
The three terms can be identified as the gravitational potential
redshift, the Doppler effect due to motion of the emitter and
receiver, and an extra effect due to the time dependence of the metric
(see also
Stebbins 1993).
In a flat
 = 0 universe
= 0 universe
 is
constant in
time in linear theory, so the last (integral) term vanishes and in the
absence of Doppler shifts the potential change is known as the
Sachs-Wolfe effect. In this limit the Sachs-Wolfe effect is simply
the red-shifting of the photon as it climbs out of the potential on
the surface of last scattering (assuming
is
constant in
time in linear theory, so the last (integral) term vanishes and in the
absence of Doppler shifts the potential change is known as the
Sachs-Wolfe effect. In this limit the Sachs-Wolfe effect is simply
the red-shifting of the photon as it climbs out of the potential on
the surface of last scattering (assuming
 = 0 at the time of
observation). In some cases, such as with gravitational waves,
non-flat or
= 0 at the time of
observation). In some cases, such as with gravitational waves,
non-flat or
 -dominated
cosmologies, or nonlinear fluctuations, the integral term can also play
a role.
-dominated
cosmologies, or nonlinear fluctuations, the integral term can also play
a role.