Copyright © 1996 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1996. 34:
155-206 Copyright © 1996 by Annual Reviews. All rights reserved |
6.2. Galactic Encounters
There is strong observational evidence that a number of spiral
galaxies are interacting gravitationally with a neighbor. The clearest
nearby
example is M81, which is believed to have undergone a recent
encounter with NGC 3077 (probably less than 109 yr
ago). Because the orbit of NGC 3077 is approximately in the disk plane of M81, this system is
particularly well suited to simulation, and
Thomasson & Donner
(1993)
predict nonaxisymmetric velocities of order 10 km s-1 in the
disk of M81. With
 t ~
1026 cm2 s-1 and
L ~ 1 kpc, the magnetic Reynolds number UL /
t ~
1026 cm2 s-1 and
L ~ 1 kpc, the magnetic Reynolds number UL /
 t is
then about 30, quite large enough to affect significantly the disk fields
(Vallée 1986).
Interestingly, M81 appears to have a strong
bisymmetric field component. M33 also may have some bisymmetric field
structure, and it is believed to be interacting with M31. Recently, at
least weak evidence has been found for BSS in the interacting
galaxy NGC 2276
(Hummel & Beck
1995)
and for MSS in M51 (EM Berkhuijsen et al, in preparation).
t is
then about 30, quite large enough to affect significantly the disk fields
(Vallée 1986).
Interestingly, M81 appears to have a strong
bisymmetric field component. M33 also may have some bisymmetric field
structure, and it is believed to be interacting with M31. Recently, at
least weak evidence has been found for BSS in the interacting
galaxy NGC 2276
(Hummel & Beck
1995)
and for MSS in M51 (EM Berkhuijsen et al, in preparation).
If we consider a Fourier decomposition of
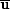 and
and
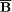 into parts
into parts
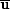 m,
m,
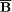 m,
corresponding to an azimuthal
wave number m, then the induction term
m,
corresponding to an azimuthal
wave number m, then the induction term
 ×
(
×
(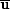 ×
×
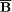 )
can give rise to a bisymmetric field component in two
ways. If the dynamo basically generates an axisymmetric field
)
can give rise to a bisymmetric field component in two
ways. If the dynamo basically generates an axisymmetric field
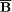 0, then
0, then
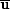 1 can
generate a slaved m = 1 component
1 can
generate a slaved m = 1 component
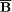 1 from the
1 from the
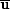 1 ×
1 ×
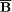 0
interaction.
Moss et al (1993b)
investigated this possibility in a nonlinear model
with a relatively thick disk, using a velocity field based on the
Thomasson & Donner
(1993)
simulation. They found that a
globally modest bisymmetric field component could be generated,
concentrated to the outer part of the disk, where it may dominate.
More subtly, the
0
interaction.
Moss et al (1993b)
investigated this possibility in a nonlinear model
with a relatively thick disk, using a velocity field based on the
Thomasson & Donner
(1993)
simulation. They found that a
globally modest bisymmetric field component could be generated,
concentrated to the outer part of the disk, where it may dominate.
More subtly, the
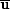 2 ×
2 ×
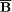 1
interaction (giving
rise directly to m = 1 and m = 3 field components) may be
such as to
increase the linear growth rate of the bisymmetric field component
compared to that of the axisymmetric component, so that in the nonlinear
case a substantial bisymmetric field could survive.
Moss (1995) showed that,
in a simple linear model, the m = 1 field could then be excited at
lower dynamo number than the m = 0 field, but a nonlinear
investigation using a
more realistic model is needed to clarify the importance of this
mechanism. The remarks concerning the modal interactions apply,
of course, whatever the mechanism providing the velocity field.
In particular, it may be relevant that a
1
interaction (giving
rise directly to m = 1 and m = 3 field components) may be
such as to
increase the linear growth rate of the bisymmetric field component
compared to that of the axisymmetric component, so that in the nonlinear
case a substantial bisymmetric field could survive.
Moss (1995) showed that,
in a simple linear model, the m = 1 field could then be excited at
lower dynamo number than the m = 0 field, but a nonlinear
investigation using a
more realistic model is needed to clarify the importance of this
mechanism. The remarks concerning the modal interactions apply,
of course, whatever the mechanism providing the velocity field.
In particular, it may be relevant that a
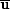 2 ×
2 ×
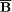 0 interaction
can give rise to a slaved m = 2 field component.
0 interaction
can give rise to a slaved m = 2 field component.