Annu. Rev. Astron. Astrophys. 1996. 34: 155-206 Copyright © 1996 by Annual Reviews. All rights reserved

8.3. Spiral Field Lines and Pitch Angles

Plane-parallel magnetic fields with a dominant azimuthal component prevail in spiral galaxies (see Section 3). This can be easily understood because differential rotation is strong in spiral galaxies (whether or not dynamos operate).

Dynamo theory predicts (Baryshnikova et al 1987), and observations of external galaxies show (Section 3.3), that the regular magnetic field must have the shape of a spiral, whether or not it is axisymmetric. Unlike spiral magnetic fields, a circular field produced within the galaxy (i.e. not supported by external currents) can not be maintained by any velocity field against turbulent magnetic diffusion. On average, the field must be a trailing spiral because differential rotation is important in producing from _r. Of course, this does not preclude local deviations from a trailing spiral pattern, as observed, e.g. in M51 (Figure 1).

The pitch angle of the magnetic field p is a readily observable parameter sensitive to details of the mechanism of magnetic field generation. Hence the magnetic pitch angle is an important diagnostic tool for theories of galactic magnetic fields. Magnetic pitch angles in spiral galaxies are observed to lie in the range p = -(10°-35°) (Figure 8). Galactic dynamo models even without spiral arms predict that p is close to these values (Krasheninnikova et al 1989, Donner & Brandenburg 1990, Elstner et al 1992, Panesar & Nelson 1992). A simple estimate for a kinematic dynamo in a thin axisymmetric disk gives (Krasheninnikova et al 1989)

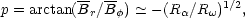(11)

and p -20° under typical conditions. Note that _r and have opposite signs because of the action of differential rotation, and so p is negative (a trailing spiral). Asymptotic kinematic dynamo models using observed rotation curves have been applied to particular galaxies (see Ruzmaikin et al 1988a); the results agree fairly well with observations. Schultz et al (1994) discuss the dependence of the pitch angle on other parameters of turbulence.

Figure 8. Observed radial variation of the magnetic pitch angle in the galaxy's plane averaged over azimuthal angle for several nearby spiral galaxies. (From Beck 1993.)

It follows from Equations (3), (6), and (11) that p -l / h (with l as the turbulent scale). The pitch angle |p| thus decreases with r when l = const, and h increases with r. This behavior is also typical of dynamos in a flat disk (Elstner et al 1992, Panesar & Nelson 1992) and is observed in spiral galaxies, as shown in Figure 8. The only exceptions are M81 and possibly also M33, both of which are candidates for bisymmetric magnetic structures due to interaction with companion galaxies (see Section 8.2).

As discussed in Section 3, magnetic pitch angles in spiral galaxies are surprisingly close to those of optical spiral arms, p_SA. Taken literally, Equation (11) implies that the equality p p_SA is a mere quantitative coincidence because the two depend on different physical parameters. Numerical simulations of the -dynamo with spiral shock waves (Panesar & Nelson 1992) show that p is quite insensitive to the presence of the shocks. The interplay between the magnetic and spiral patterns is far from being completely understood (Section 8.4) and, possibly, there are deeper physical reasons for the observed correspondence of the pitch angles.

Concerning the primordial field theory, a straightforward idea is that the pitch angle of a magnetic field frozen into a differentially rotating disk is a decreasing function of time and, after N revolutions (with N 30 for the Solar vicinity in the Milky Way), we have p -N^-1 rad -2°, so that |p| << |p_SA|. Furthermore, |p| grows with r insofar as angular velocity decreases with r - a trend opposite to that observed.

We note that the ASS fields observed in the spiral galaxies M31 and IC 342 and the magnetic spiral arms in NGC 6946 are directed inwards. For the edge-on galaxy NGC 253, a similar conclusion follows if one assumes that the magnetic field is also aligned with the spiral arms. As the direction of a dynamo-generated field is determined by that of the initial field, this dominance, if it were to be confirmed by better statistics, might clarify the nature of the seed field. For example, it could indicate the importance of battery effects (relying on galactic rotation). Within the framework of the primordial field theory, such a dominance would imply a hardly plausible correlation between the directions of the intergalactic field and the sense of galactic rotation.