4.5. Yet Further Constraints: Spectroscopy

So far, and mainly for technical reasons, the most important constraints on lens models were coming from imaging. Spectroscopy is nevertheless another key component, that will become of growing importance in the near future, thanks to 3D spectrographs mounted on large telescopes.

Spectroscopy provides independent access to the total mass of the lenses: whenever an intervening cluster or group is seen close to the line of sight to a lens, measuring its velocity dispersion helps to break the mass sheet degeneracy it introduces with the mass of the main lens (e.g., Falco et al. 1997; Tonry 1998; Kneib et al. 2000). If a measurement of the velocity dispersion of the main lens is available as well, the effect of the mass sheet degeneracy is greatly minimized In the case of PG 1115+080, both the velocity dispersion of the main lens and nearby group are available (see Table 1).

Table 1. Summary of the observational saga of PG 1115+080 since the time-delay measurement, and estimates for H₀ (along with the 1 errors, when available) while the observations improve.

Reference	Observational or	H0
	theoretical improvement	(km s-1 Mpc-1)
Schechter et al. (1997)	Time delay measurement:
	(CB) = 23.7 ± 3.4 days	42 or 84
	(CA) = 9.4 days
Barkana (1997)	Redetermination of
	time-delays (Schechter's data):	no new
	(CB) = 25+3.3-3.8 days	estimate
	(CA) = 13 days
Kundic et al. (1997)	Redshifts of the lens
	and group:	52 ± 14
	zlens = zgroup = 0.311
	group = 270 ± 70 km/s
Saha & Williams (1997)	Non parametric models including
	main lens plus group. Explore
	broad range of lens mass profiles	42, 63, or 84
	and ellipticities.
Keeton & Kochanek (1997)	Parametric models including
	main lens and group. Explore	51+14-13
	broad range of lens shapes.
Courbin et al. (1997)	Improved astrometry from
	ground based imaging.	53+10-7
Impey et al. (1998)	New HST/NICMOS images.
	Discover lensed ring.	44 ± 4 or 65 ± 5
	Improved astrometry and lens
	ellipticity.
Tonry (1998)	Velocity dispersion of
	the lens and group:
	lens = 281 ± 25 km/s
	group = 326 km/s
Treu & Koopmans (2002)	Use dynamical info on the
	lens and group to break	59+12-7 ( ± 3 syst)
	degeneracies between models

For an isothermal sphere the line of sight velocity dispersion is directly related to the Einstein radius, through the H₀ independent relation:

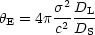(6)

Since the Einstein radius _E only depends on the total mass of the lens (within the Einstein radius), measuring the velocity dispersion does not yield the mass profile of the lens. Nevertheless, it can be used to put strong constraints on the mass profile, using further knowledge we have on galaxies in general. Treu & Koopmans (2002) take the problem under this view angle and feed dynamical models of galaxies with the measured velocity dispersions in PG 1115+080. In their model, the lensing galaxy is composed of a dark matter halo with a mass density profile of the form (r) = r^- ( = 1 for a Navarro, Frenk & White (1997) profile) and a Jaffe stellar density profile (Jaffe 1983). New parameters appear in the model: the slope or the dark matter halo, and the fraction of the galaxy that is under the form of (luminous) stars, f_*. However, (, f_*) define a parameter space with a rather sharp peak, centered at ~ 2.35 and f_* ~ 0.67, for PG 1115+080. There is therefore a rather small range of lens models that fit simultaneously the physical properties of the lens, and the constraints imposed by lensing. Using this approach leads to H₀ = 59⁺¹²_-7 km s^-1 Mpc^-1, a value which is much less affected by systematic errors than other estimates, not taking the dynamical information into account.

Measuring velocity dispersions in faint objects in not easy, especially when they are blended with bright quasar images. It has been possible, so far, only for a few systems, but spectrographs are starting to be used on large telescopes where adaptive optics observations are carried out in a flexible way. Three-dimensional spectrographs are planed on these telescopes, and may well yield not only the velocity dispersion of lenses, but also their full velocity field. In many cases, one will be able to measure at least the velocity dispersion profile, hence constraining much better the mass profile of the lens, independent of lensing.