


Measuring time-delays has long been the main limitation to the use of quasar lenses in cosmology. Indeed, obtaining on a regular basis images of good quality and for long period of time is not easy. With the increasing number of large telescopes in excellent sites, and operated in "service mode", we have nevertheless entered a phase of mass production of time-delays. It took more than a decade to obtain the time-delay in Q 0957+561, but four time-delays were recently measured in one single thesis (Burud, 2000b) thanks to modern instrumentation and image deconvolution techniques. In addition, systematic imaging campaigns of lensed quasars such as the one carried out by CASTLE, facilitate the modeling of lens galaxies. Deep HST images are used in combination with spectroscopy, and along with what we know of the physics/dynamics of galaxies, to break the degeneracies between the models.
Even if the observational situation in quasar lensing is expected to improve a lot in the coming years, thanks to adaptive optics and 3D spectrographs, we can already say, with the precision of the observations collected so far, that lensed quasars are at least as powerful as other methods to determine H0.
Let us play the naive game that consists in taking from literature the
nine estimates of H0, for each of the nine measured time-delays,
and average them. This is summarized in Table 2
for all known lenses,
along with the time-delay measurements. We indicate in the table the
value obtained for H0 with all kind of different models, just
scaling the published errors to
1 . Some authors consider
isothermal spheres or ellipsoids with and without external shear.
Others prefer to use lenses with constant mass-to-light ratios. In
other words, the values we quote in Table 2 are
all affected by
unknown systematics. These systematics have been estimated by each
author and included in the published error bars. If they had been
under- or over- estimated, the dispersion between all the individual
estimates of H0, and the published errors on one single
measurement, would be incompatible. Following our naive idea the
averaged value for H0, (without error weighting) is
H0 = 61 ± 7
km s-1 Mpc-1. Figure 12
is another way of displaying the data of Table 2,
showing the value of H0 as a function of the lens redshift. The
1
. Some authors consider
isothermal spheres or ellipsoids with and without external shear.
Others prefer to use lenses with constant mass-to-light ratios. In
other words, the values we quote in Table 2 are
all affected by
unknown systematics. These systematics have been estimated by each
author and included in the published error bars. If they had been
under- or over- estimated, the dispersion between all the individual
estimates of H0, and the published errors on one single
measurement, would be incompatible. Following our naive idea the
averaged value for H0, (without error weighting) is
H0 = 61 ± 7
km s-1 Mpc-1. Figure 12
is another way of displaying the data of Table 2,
showing the value of H0 as a function of the lens redshift. The
1 error region is dashed
on the figure. Four measurements (in
fact 3, if we include the mean value for the 2 estimates for
HE 1104-1805 in the dashed area) are outside the
1
error region is dashed
on the figure. Four measurements (in
fact 3, if we include the mean value for the 2 estimates for
HE 1104-1805 in the dashed area) are outside the
1 region, as
expected for 9 independent measurements. Unless all the authors did
the same systematic error (and this is unlikely because of the very
different choices of models), the dispersion between the points is
fully compatible with the individual error bars. This means that even
if the models suffer from systematics, the amplitude of the error has
been correctly estimated by the authors.
region, as
expected for 9 independent measurements. Unless all the authors did
the same systematic error (and this is unlikely because of the very
different choices of models), the dispersion between the points is
fully compatible with the individual error bars. This means that even
if the models suffer from systematics, the amplitude of the error has
been correctly estimated by the authors.
| Object | Time-delay(s) | H0 |
| (leading image first) | (km s-1 Mpc-1) | |
| B 0218+357 | ||
| Biggs et al. (1999) |
 (BA) = 10.5
± 0.2 days (2%) (BA) = 10.5
± 0.2 days (2%) |
69+7-9 |
| RX J0911+0551 | ||
| Hjorth et al. (2002) |
 (BA) = 146
± 4 days (3%) (BA) = 146
± 4 days (3%) |
71 ± 2 ( ± 4 syst) |
| Q 0957+561 | ||
| Kundic et al. (1997) |
 (BA) = 417
± 0.6 days (0.15%) (BA) = 417
± 0.6 days (0.15%) |
64 ± 7 |
| but multiple time-delays | ||
| Goicoechea (2002) |
 (BA) = 425
± 4.0 days (1.0%) (BA) = 425
± 4.0 days (1.0%) |
|
 (BA) = 432
± 1.9 days (0.5%) (BA) = 432
± 1.9 days (0.5%) |
||
| HE 1104-1805 | Strong micro/milli-lensing | |
| Gil-Merino et al. (2002) |
 (AB) = 310
± 9 days (3%) (AB) = 310
± 9 days (3%) |
48 ± 2 or 62 ± 2 |
| PG 1115+080 | ||
| Schechter et al. (1997) |
 (CB) =
25+3.3-3.8 days (14%) (CB) =
25+3.3-3.8 days (14%) |
|
| Barkana (1997) |
 (CA) = 13
days (CA) = 13
days |
|
| Treu & Koopmans (2002) | 59 +12-7 ( ± 3 syst) | |
| SBS 1520+53 | ||
| Burud et al. (2002) |
 (BA) = 130
± 3 days (3%) (BA) = 130
± 3 days (3%) |
51 ± 9 |
| B 1600+434 | Radio and optical time-delays | |
| Koopmans et al. (2000) |
 (BA) = 47
± 5 days (10%) (BA) = 47
± 5 days (10%) |
57+7-6 |
| Burud et al. (2000) |
 (BA) = 51
± 2 days (4%) (BA) = 51
± 2 days (4%) |
52+7-4 |
| B 1608+656 | ||
| Fassnacht et al. (2002) |
 (BA) = 31.5
± 2 days (6%) (BA) = 31.5
± 2 days (6%) |
63 ± 15 |
 (BC) = 36.0
± 2 days (6%) (BC) = 36.0
± 2 days (6%) |
||
 (BD) = 77.0
± 3 days (4%) (BD) = 77.0
± 3 days (4%) |
||
| PKS 1830-211 | No estimate. Lens | |
| Lovell et al. (1998) |
 (BA) =
26+4-5 days (17%) (BA) =
26+4-5 days (17%) |
may be multiple |
| HE 2149-2745 | ||
| Burud et al. (2002b) |
 (BA) = 103
± 12 days (11%) (BA) = 103
± 12 days (11%) |
65 ± 8 |
| COMBINED | 61 ± 7 | |
A more correct approach is to impose that a given family of profiles
is used to model the mass distribution of lenses in general, and to
impose that H0 should be the same everywhere in the
Universe. This has been done so far by very few authors.
Williams & Saha
(2000),
use two systems and their non-parametric models, to infer
H0 = 61 ± 11 km s-1
Mpc-1(1 error).
Courbin et al. (2002)
add two other lenses to the Williams & Saha sample, and adopt the same
non-parametric technique to infer H0 = 64 ± 4 km
s-1 Mpc-1. Using
parametric lens models and a set of 4 different lenses (only
PG 1115+080 is common to all authors)
Kochanek (2002)
obtain H0 = 51 ± 5
km s-1 Mpc-1if lens galaxies have dark matter
halos, or H0 = 73 ± 8
km s-1 Mpc-1 if lens galaxies have constant
mass-to-light ratios.
error).
Courbin et al. (2002)
add two other lenses to the Williams & Saha sample, and adopt the same
non-parametric technique to infer H0 = 64 ± 4 km
s-1 Mpc-1. Using
parametric lens models and a set of 4 different lenses (only
PG 1115+080 is common to all authors)
Kochanek (2002)
obtain H0 = 51 ± 5
km s-1 Mpc-1if lens galaxies have dark matter
halos, or H0 = 73 ± 8
km s-1 Mpc-1 if lens galaxies have constant
mass-to-light ratios.
Gravitationally lensed quasars have one drawback over other methods
for determining H0: they do require good knowledge of the mass
profile of the lens. It has long been a limitation to the
effectiveness of the method to produce reliable estimates of H0,
but this drawback is becoming easier and easier to overcome, thanks to
spectroscopy, to high spatial resolution observations, and to the
progresses made on the physics of galaxies. Gravitational lenses have,
on the other hand, tremendous advantages over other methods. First,
they do not rely on any "standard candle" which would rend the
method close to useless if the standard candle turned out to be
significantly deviant from the "standard" behaviour. Second, it does
not require secondary calibrators of the standard candle, e.g., low
redshift objects, in the case of the supernovae method. Third, it
probes H0 at cosmological distances, independent of any local
effect such as peculiar velocities of nearby galaxies. Finally,
lensing is not as sensitive to the other cosmological parameters
( m,
m,

 )
than the other methods.
)
than the other methods.
We compare in Fig. 12, the value of
H0 for lensed quasars and for
the Cepheid method. With the present error bars, calculated with only
9 objects, we can say that lensed quasars and Cepheid
disagree. Lensing gives lower values for H0 than does the Cepheid
method. If our knowledge of the mass distribution of galaxies is any
good, i.e., that galaxies have dark matter halos, the lensing value
would be even smaller. Recent CMB experiments such as WMAP find high
values for H0 (e.g.,
Spergel et al. 2003),
in agreement with the local
estimate: H0 = 71, with impressive error bars of only 4%. With
the high degree of degeneracy between the cosmological models used to
represent the observed CMB power spectrum, H0 is in fact shown to
take any value between 54 and 72
(Efstathiou 2003).
It spans over an even broader ranger if one does not invoke any prior
knowledge on the value of
 m and
m and

 as
determined with supernovae.
as
determined with supernovae.
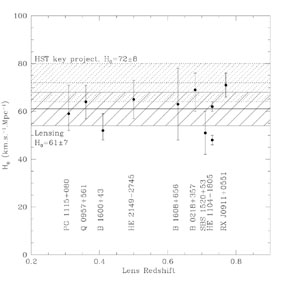 |
Figure 12. Values of H0 for all lenses with known time-delays. H0 is given as a function of lens redshift, directly taken from the literature. The dashed area shows the range of possible values, according to lensing, which is to be compared with the dashed-dotted area, infered from the Cepheid method in the framework of the HST key project. As in the case of PG 1115+080, the mean value for H0 is very marginally compatible with the local estimate of the Hubble parameter. |
In fact, no single method has been proved to be good enough that it can surpass the others. There are, however, methods that are better than others as pinning down some of the cosmological parameters and it has been emphasized many times (Bridle et al. 2003) that all methods should be combined in order to break the degeneracies inherent to one specific method. Gravitational lensing is one of these methods. It has advantages and drawbacks, but probably many more advantages than drawbacks given the present observational context.
Acknowledgements. The author wishes to thank Alain Smette and Pierre Magain for useful discussions. Frédéric Courbin is supported by the European Commission through a Marie Curie Individual Fellowship, under grant MCFI-2001-0242. The collaborative grant ECOS/CONICYT C00U05 between Chile and France is also gratefully acknowledged.