2. TAKING THE MEASURE OF THE UNIVERSE

2.1. Cosmological Framework

The framework for understanding the evolution of the universe is the hot big-bang model, technically referred to as the Friedmann-Lemaitre-Robertson-Walker (FLRW) cosmological model. Grounded in Einstein's theory of general relativity, this model assumes that on the largest scales the universe is homogeneous and isotropic, features which have now been confirmed observationally.

The FLRW model incorporating inflation, can be described by 16 cosmological parameters that we group here into two categories (see Table I). The first 10 parameters describe the expansion, the global geometry, the age and the composition of the underlying FLRW model, while the final 6 describe the deviations from exact homogeneity, which at early times were small, but today manifest themselves in the abundance of cosmic structure, from galaxies to superclusters.

Table 1. OUR 16 COSMOLOGICAL PARAMETERS

Parameter	Value 1	Description	WMAP 2
		Ten Global Parameters
h	0.72 ± 0.07	Present expansion rate 3	0.71+0.04-0.03
q0	-0.67 ± 0.25	Deceleration parameter 4	-0.66 ± 0.10 5
t0	13 ± 1.5 Gyr	Age of the Universe 6	13.7 ± 0.2 Gyr
T0	2.725 ± 0.001 K	CMB temperature 7
0	1.03 ± 0.03	Density parameter 8	1.02 ± 0.02
B	0.039 ± 0.008	Baryon Density 9	0.044 ± 0.004
CDM	0.29 ± 0.04	Cold Dark Matter Density 9	0.23 ± 0.04
	0.001 - 0.05	Massive Neutrino Density 10
X	0.67 ± 0.06	Dark Energy Density 9	0.73 ± 0.04
w	-1 ± 0.2	Dark Energy Equation of State 11	< -0.8 (95% cl)
		Six Fluctuation Parameters
S	5.6+1.5-1.0 × 10-6	Density Perturbation Amplitude 12
T	< S	Gravity Wave Amplitude 13	T < 0.71S (95%cl)
8	0.9 ± 0.1	Mass fluctuations on 8 Mpc 14	0.84 ± 0.04
n	1.05 ± 0.09	Scalar index 8	0.93 ± 0.03
nT	--	Tensor index
dn / d ln k	-0.02 ± 0.04	Running of scalar index 15	-0.03 ± 0.02
1 The 1- uncertainties quoted in this table represent our combined analysis of published data. 2 Bennett et al., 2003. 3 Freedman et al., 2001; note: H0 = 100h km sec-1 Mpc-1. 4 Supernovae results combined with measurements of the total matter density, M = + B + CDM and 0, assuming w = - 1 (Perlmutter et al., 1999, Riess et al., 1998). 5 WMAP results (Bennett et al., 2003) combined with Tonry et al., 2003. 6 Value based upon CMB, globular cluster ages and current expansion rate (Knox et al., 2001, Krauss and Chaboyer, 2002, Oswald et al., 1996). 7 Mather et al. 1999. 8 Combined analysis of four CMB measurements (Sievers et al., 2002). 9 Combined analysis of CMB, BBN, H0 and cluster baryon fraction (Turner, 2002). 10 Lower limit from SuperKamiokande measurements; upper limit from structure formation (Fukuda et al., 2002, Elgaroy et al., 2002). 11 Supernova measurements, CMB and large-scale structure (Perlmutter et al., 1999). 12 Contribution of density perturbations to the variance of the CMB quadrupole (with T = 0) (Gorski et al., 1996). 13 Contribution of gravity waves to the variance of the CMB quadrupole (upper limit) (Kinney et al., 2001). 14 Variance in values reported is larger than the estimated errors; adopted error reflects this (Lahav et al., 2002). 15 Deviation of the scalar perturbations from a pure power law (Lewis and Bridle, 2002).

The Friedmann equation governs the expansion rate and relates several of the first 10 parameters:

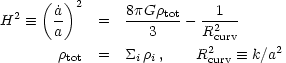(1)

where H is the expansion rate, a(t) is the cosmic scale factor (which describes the separation of galaxies during the expansion), _tot is the mass-energy density, and R_curv is the curvature radius. The well known cosmological redshift z (which relates the observed wavelength of a photon _R when received at time t_R, to its restframe wavelength _E when emitted at time t_E) is directly tied to the change in cosmic scale factor a(t): 1 + z _R / _E = a(t_R) / a(t_E).

From the Friedmann equation it follows that the total mass-energy and spatial curvature k are linked:

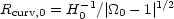(2)

where the subscript `0' denotes the current value of the parameter, _{0 tot} / _crit and _crit 3H₀² / 8G is the so-called "critical density" that separates positively curved (k > 0), high-density universes from negatively curved (k < 0), low-density universes. Recent measurements of the anisotropy of the cosmic microwave background have provided convincing evidence that the spatial geometry is very close to being uncurved (flat, k = 0), with ₀ = 1.0 ± 0.03 (deBernardis et al., 2002).

The currently known components of the Universe include ordinary matter or baryons (_B = _B / _crit), cold dark matter (_CDM), massive neutrinos (), the cosmic microwave background and other forms of radiation (_rad), and dark energy (_X). The values for these densities are derived empirically, as discussed below, and sum, to within their margins of error, to the critical density, ₀ = 1, consistent with the determination of the curvature, k = 0.

The second set of parameters, which broadly characterize the individual deviations from homogeneity, describe (a) the tiny (~ 0.01%) primeval fluctuations in the matter density as encoded in the CMB, (b) the inhomogeneity in the distribution of matter today, and (c) the possible spectrum of gravitational waves produced by inflation. The initial spectrum of density fluctuations is described in terms of its power spectrum P(k), which is the square of the Fourier transform of the density field, P(k) |_k|², where the wavenumber k is related to the wavelength of the fluctuation, k = 2 / . (Galaxies like ours are formed from perturbations of wavelength ~ 1 Mpc.) The primordial power spectrum is described by a power law, P(k) kⁿ, where a power index n = 1.0 corresponds to fluctuations in the gravitational potential that are the same on all scales (so-called scale invariant). The scale-invariant spectrum is predicted by inflation and agrees well with current observations. The overall amplitude of the density perturbations can be described by either S, the CMB quadrupole anisotropy produced by the fluctuations or ₈, the amplitude of fluctuations on a scale of 8h^-1 Mpc, which is found from observations to be of order unity.

Accurately measuring these parameters presents a significant challenge. As we now describe, thanks to major advances in technology, the challenge is being met, and in some cases, with independent measurements that check the consistency of both the theoretical framework, and the results themselves.