


2.6. The Age of the Universe
The time back to the big bang depends upon H0 and the expansion history, which itself depends upon the composition:
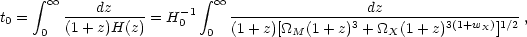 |
where  M =
M =
 CDM +
CDM +
 B +
B +

 is the total mass density.
is the total mass density.
For a universe with a Hubble constant of 72 km sec-1 Mpc-1 and matter contributing 1/3 and dark energy 2/3 to the overall mass-energy density, the time back to the big bang is 13Gyr. Taking account of the uncertainties in H0 and the composition, the uncertainty in the age of the universe is estimated to be about ± 1.5Gyr. The expansion age can also be determined from CMB anisotropy, but without recourse to H0, and it gives a consistent age, t0 = 14 ± 0.5 Gyr (Knox et al., 2001).
The expansion age can also be checked for consistency against other cosmic clocks. For example, the best estimates of the age of the oldest stars in the universe are obtained from systems of 105 or so stars known as globular clusters. Stars spend most of their lifetimes undergoing nuclear burning of hydrogen into helium in their central cores. Detailed computer models of stellar evolution matched to observations of globular-cluster stars yield ages of about 12.5 billion years, with an uncertainty of about 1.5Gyr (Krauss and Chaboyer, 2002). These estimates are also in good agreement with other methods that independently measure the rates of cooling of the oldest white dwarf stars, and techniques that use various radioactive elements as cosmic chronometers (Oswald et al., 1996). Finally, with the assumption that wX = - 1, the type Ia supernova data can constrain the product of the age and Hubble constant independent of either quantity, H0 t0 = 0.96 ± 0.04 (Tonry et al., 2003). This is consistent with the product of the two, (H0 = 72 ± 8 km sec-1 Mpc-1) × (t0 = 13 ± 1.5 Gyr) = 0.96 ± 0.16.
In summary, all the ages for the universe are consistent with a consensus age of about 13 ± 1.5 Gyr.