


Inflation can be described simply as any period of the Universe's
evolution in which the size of the Universe
is accelerating. This surprisingly simple type of expansion leads to our
observed universe without invoking special initial conditions.
The active ingredient of the inflationary remedy to the structure,
horizon and flatness problems
is rapid exponential expansion sometime within the first picosecond ( =
trillionth of a second = 10-12 s) after the big bang.
If the structure, flatness and horizon problems are so easily solved,
it is important to understand how this quick cure works.
It is important to understand the details of expansion and cosmic horizons.
Also, since our Universe is becoming more
 -dominated every
day (Fig. 3),
we need to prepare for the future. Our descendants will, of necessity,
become more and more
familiar with inflation, whether they like it or not. Our Universe is
surrounded by inflation at both ends of time.
-dominated every
day (Fig. 3),
we need to prepare for the future. Our descendants will, of necessity,
become more and more
familiar with inflation, whether they like it or not. Our Universe is
surrounded by inflation at both ends of time.
2.1. Friedmann-Robertson-Walker metric
 Hubble's law
and Cosmic Event Horizons
Hubble's law
and Cosmic Event Horizons
The general relativistic description of an homogeneous, isotropic universe is based upon the Friedmann-Robertson-Walker (FRW) metric for which the spacetime interval ds, between two events, is given by
![\begin{equation}
ds^2 = -c^2dt^2 + R(t)^2[d\chi^2+S_k^2(\chi)d\psi^2],
\end{equation}](Equations/eq0x.gif) |
(1) |
where c is the speed of light, dt is the time separation,
d is the comoving
coordinate separation and
d
is the comoving
coordinate separation and
d 2 =
d
2 =
d 2 +
sin2
2 +
sin2
 d
d 2, where
2, where
 and
and
 are the polar
and azimuthal angles in
spherical coordinates. The scale factor R has dimensions of
distance. The function
Sk(
are the polar
and azimuthal angles in
spherical coordinates. The scale factor R has dimensions of
distance. The function
Sk( ) =
sin
) =
sin ,
,
 or
sinh
or
sinh for closed (positive
k), flat (k = 0) or
open (negative k) universes respectively (see e.g.
Peacock 1999
p. 69).
for closed (positive
k), flat (k = 0) or
open (negative k) universes respectively (see e.g.
Peacock 1999
p. 69).
In an expanding universe, the proper distance D between an
observer at the origin and a
distant galaxy is defined to be along a surface of constant time
(dt = 0). We are interested in the radial distance so
d = 0. The FRW metric
then reduces to
ds = Rd
= 0. The FRW metric
then reduces to
ds = Rd which,
upon integration, becomes,
which,
upon integration, becomes,
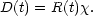 |
(2) |
Taking the time derivative and assuming that we are dealing with a comoving
galaxy (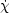 = 0) we have,
= 0) we have,
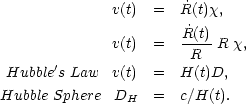 |
(3) (4) (5) (6) |
The Hubble sphere is the distance at which the recession velocity
v is equal to the speed of light.
Photons have a peculiar velocity of
c = 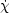 R,
or equivalently photons move through comoving space with a velocity
R,
or equivalently photons move through comoving space with a velocity
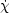 = c /
R. The comoving distance traveled by a photon is
= c /
R. The comoving distance traveled by a photon is

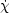 dt, which we can use to define the comoving coordinates of some
fundamental concepts:
dt, which we can use to define the comoving coordinates of some
fundamental concepts:
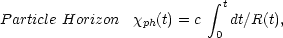 |
(7) |
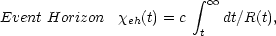 |
(8) |
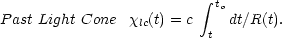 |
(9) |
Only the limits of the integrals are different. The horizons, cones and spheres of Eqs. 6 - 9 are plotted in Fig. 1.
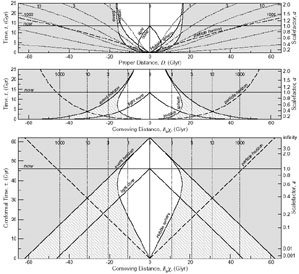 |
Figure 1. Expansion of the Universe.
We live on the central vertical worldline.
The dotted lines are the worldlines of galaxies being expanded away
from us as the Universe expands. They are labeled by the redshift of
their light that is reaching us today, at the apex of our past light cone.
Top: In the immediate past our past light cone is shaped like a
cone. But as we follow it further into the past it curves in and makes
a teardrop shape. This is a fundamental feature of the expanding
universe; the furthest light that we can see now was receding from us
for the first few billion years of its voyage. The Hubble sphere,
particle horizon, event horizon and past light cone are also shown
(Eqs. 6 - 9). Middle: We remove the expansion of the Universe from the
top panel by plotting comoving distance on the x axis rather than
proper distance. Our teardrop-shaped light cone then becomes a
flattened cone and the constant proper distance of the event horizon
becomes a shrinking comoving event horizon - the active ingredient of
inflation (Section 2.2).
Bottom: the radius of the current observable Universe (the particle
horizon) is 47 billion light years (Glyr), i.e., the most distant
galaxies that we can see on our past light cone are now 47 billion
light years away. The top panel is long and skinny because the Universe
is that way - the Universe is larger than it is old - the particle
horizon is 47 Glyr while the age is only 13.5 Gyr - thus producing the
3 : 1( |