Inflation and the CMB - C.H. Lineweaver

3. FRIEDMANN OSCILLATIONS: THE RISE AND FALL OF DOMINANT COMPONENTS

Friedmann's Equation can be derived from Einstein's 4×4 matrix equation of general relativity (see for example Landau & Lifshitz 1975, Kolb and Turner 1992 or Liddle & Lyth 2000):

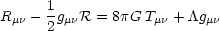$\begin{equation} R_{\mu \nu} - \frac{1}{2}g_{\mu \nu} {\mathcal R} = 8\pi G\; T_{\mu \nu} + \Lambda g_{\mu \nu} \end{equation}$

(10)

where R_µ is the Ricci tensor, is the Ricci scalar, g_µ is the metric tensor describing the local curvature of space (intervals of spacetime are described by ds² = g_µ dx^µ dx), T_µ is the stress-energy tensor and Lambda is the cosmological constant. Taking the (µ, ) = (0, 0) terms of Eq. 10 and making the identifications of the metric tensor with the terms in the FRW metric of Eq. 1, yields the Friedmann Equation:

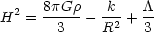$\begin{equation} H^{2} = \frac{8\pi G \rho}{3} - \frac{k}{R^{2}} + \frac{\Lambda}{3}\\ \end{equation}$

(11)

where R is the scale factor of the Universe, H = dot{R} / R is Hubble's constant, rho is the density of the Universe in relativistic or non-relativistic matter, k is the constant from Eq. 1 and Lambda is the cosmological constant. In words: the expansion (H) is controlled by the density ( rho ), the geometry (k) and the cosmological constant ( Lambda ). Dividing through by H² yields

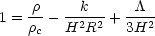$\begin{equation} 1 = \frac{\rho}{\rho_{c}} - \frac{k}{H^{2}R^{2}} + \frac{\Lambda}{3H^{2}} \end{equation}$

(12)

where the critical density rho _c = 3 H² / 8 G. Defining Omega = rho / rho _c and Omega = Lambda / 3H² and using Omega = Omega + Omega we get,

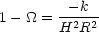$\begin{equation} 1 - \Omega = \frac{-k}{H^{2}R^{2}} \end{equation}$

(13)

or equivalently,

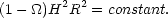$\begin{equation} (1 - \Omega)H^{2}R^{2} = constant. \end{equation}$

(14)

If we are interested in only post-inflationary expansion in the radiation- or matter-dominated epochs we can ignore the Lambda term and multiply Eq. 11 by 3 / 8 G rho to get

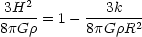$\begin{equation} \frac{3H^{2}}{8\pi G \rho} = 1 - \frac{3k}{8\pi G \rho R^{2}} \end{equation}$

(15)

which can be rearranged to give

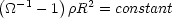$\begin{equation} \left(\Omega^{-1} - 1\right)\rho R^{2} = constant \end{equation}$

(16)

A more heuristic Newtonian analysis can also be used to derive Eqs. 14 & 16 (e.g. Wright 2003). Consider a spherical shell of radius R expanding at a velocity v = HR, in a universe of density rho . Energy conservation requires,

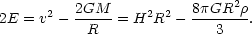$\begin{equation} 2E = v^{2} - \frac{2GM}{R}= H^{2}R^{2} - \frac{8\pi G R^{2}\rho}{3}. \end{equation}$

(17)

By setting the total energy equal to zero we obtain a critical density at which v = HR is the escape velocity,

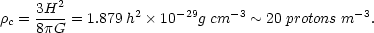$\begin{equation} \rho_{c} = \frac{3 H^{2}}{8 \pi G} = 1.879 \;h^{2} \times 10^{-29} g\; cm^{-3} \sim 20\; protons\; m^{-3}. \end{equation}$

(18)

However, by requiring only energy conservation (2E = constant not necessarily E = 0) in Eq. 17, we find,

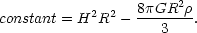$\begin{equation} constant = H^{2}R^{2} - \frac{8\pi G R^{2}\rho}{3}. cm^{-3} \sim 20\; protons\; m^{-3}. \end{equation}$

(19)

Dividing Eq. 19 by H² R² we get

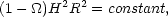$\begin{equation} (1 - \Omega)H^{2}R^{2} = constant, \end{equation}$

(20)

which is the same as Eq. 14. Multiplying Eq. 19 by 3 / (8 G rho R²) we get

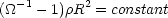$\begin{equation} (\Omega^{-1} - 1)\rho R^{2} = constant \end{equation}$

(21)

which is the same as Eq. 16.