7.8. Observational Constraints from the CMB

Our general relativistic description of the Universe can be divided into two parts, those parameters like _i and H which describe the global properties of the model and those parameters like n_s and A which describe the perturbations to the global properties and hence describe the large scale structure (Table 1).

In the context of general relativity and the hot big bang model, cosmological parameters are the numbers that, when inserted into the Friedmann equation, best describe our particular observable universe. These include Hubble's constant H (or h = H / 100 km s^-1 Mpc ^-1), the cosmological constant = / 3H², geometry _k = - k / H² R², the density of matter, _M = _CDM + _baryon = _CDM / _c + _baryon / _c and the density of relativistic matter _rel = + . Estimates for these have been derived from hundreds of observations and analyses. Various methods to extract cosmological parameters from cosmic microwave background (CMB) and non-CMB observations are forming an ever-tightening network of interlocking constraints. CMB observations now tightly constrain _k, while type Ia supernovae observations tightly constrain the deceleration parameter q_o. Since lines of constant _k and constant q_o are nearly orthogonal in the _M - plane, combining these measurements optimally constrains our Universe to a small region of parameter space.

The upper limit on the energy density of neutrinos comes from the shape of the small scale power spectrum. If neutrinos make a significant contribution to the density, they suppress the growth of small scale structure by free-streaming out of over-densities. The CMB power spectrum is not sensitive to such small scale power or its suppression, and is not a good way to constrain . And yet the best limits on come from the WMAP normalization of the CMB power spectrum used to normalize the power spectrum of galaxies from the 2dF redshift survey (Bennett et al. 2003).

The parameters in Table 1 are not independent of each other. For example, the age of the Universe, t_o = h^-1 f (_M, ). If _m = 1 as had been assumed by most theorists until about 1998, then the age of the Universe would be simple:

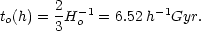(36)

However, current best estimates of the matter and vacuum energy densities are (_M, ) = (0.27, 0.73). For such flat universes ( = _M + = 1) we have (Carroll et al. 1992):

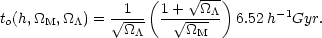(37)

for t_o(h = 0.71, _M = 0.27, = 0.73) = 13.7 Gyr.

If the Universe is to make sense, independent determinations of , _M and h and the minimum age of the Universe must be consistent with each other. This is now the case (Lineweaver 1999). Presumably we live in a universe which corresponds to a single point in multidimensional parameter space. Estimates of h from HST Cepheids and the CMB overlap. Deuterium and CMB determinations of _baryon h² are consistent. Regions of the _M - plane favored by supernovae and CMB overlap with each other and with other independent constraints (e.g. Lineweaver 1998). The geometry of the Universe does not seem to be like the surface of a ball (_k < 0) nor like a saddle (_k > 0) but seems to be flat (_k 0) to the precision of our current observations.

There has been some speculation recently that the evidence for is really evidence for some form of stranger dark energy (dubbed `quintessence') that we have been incorrectly interpreting as . The evidence so far indicates that the cosmological constant interpretation fits the data as well as or better than an explanation based on quintessence.

Table 1. Cosmological parameters describing the best-fitting FRW model to the CMB power spectrum and other non-CMB observables (cf. Bennett et al. 2003).

Composition of Universea
Total density	o	1.02 ± 0.02
Vacuum energy density		0.73 ± 0.04
Cold Dark Matter density	CDM	0.23 ± 0.04
Baryon density	b	0.044 ± 0.004
Neutrino density		< 0.0147 95% CL
Photon density		4.8 ± 0.014 × 10-5
Fluctuations
Spectrum normalizationb	A	0.833+0.086-0.083
Scalar spectral indexb	ns	0.93 ± 0.03
Running index slopeb	dns / d lnk	-0.031+0.016-0.018
Tensor-to-scalar ratioc	r = T/S	< 0.71 95% CL
Evolution
Hubble constant	h	0.71+0.04-0.03
Age of Universe (Gyr)	t0	13.7 ± 0.2
Redshift of matter-energy equality	zeq	3233+194-210
Decoupling Redshift	zdec	1089 ± 1
Decoupling epoch (kyr)	tdec	379+8-7
Decoupling Surface Thickness (FWHM)	zdec	195 ± 2
Decoupling duration (kyr)	tdec	118+3-2
Reionization epoch (Myr, 95% CL))	tr	180+220-80
Reionization Redshift (95% CL)	zr	20+10-9
Reionization optical depth		0.17 ± 0.04
a i = i / c where c = 3H2 / 8 G b at a scale corresponding to wavenumber k0 = 0.05 Mpc-1 c at a scale corresponding to wavenumber k0 = 0.002 Mpc-1