


Ever since Edwin Hubble's pioneering measurements in the 1920s (and to some extent even before that, since Vesto Slipher's measurements, that started in 1912; e.g., Slipher 1917), we knew that we live in an expanding universe (Hubble 1929, Hubble and Humason 1931). In the standard big bang theory the universe expands uniformly, with the recession velocity being related to the distance through the Hubble law, v = H0d. More generally, based on the "Cosmological Principle" (the assumption that the universe is homogeneous and isotropic on large scales), the expansion is governed by the Friedmann equation in the context of general relativity
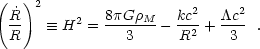 |
(24) |
Here R(t) is the scale factor,
H =  / R
measures expansion rate (with H0, the "Hubble
Constant," giving the rate at present),
/ R
measures expansion rate (with H0, the "Hubble
Constant," giving the rate at present),
 M is
the mass density, k is the curvature parameter and
M is
the mass density, k is the curvature parameter and
 is Einstein's
cosmological constant (which represents the energy density of the
vacuum). Commonly, the density of matter and that associated with the
vacuum are represented by the density parameters (at present)
is Einstein's
cosmological constant (which represents the energy density of the
vacuum). Commonly, the density of matter and that associated with the
vacuum are represented by the density parameters (at present)
 M =
8
M =
8 G
G
 M /
3H20 and
M /
3H20 and

 =
=
 c2 / 3H20, with which the
Friedmann equation can be expressed as
(kc2 / Ro2) =
H20
(
c2 / 3H20, with which the
Friedmann equation can be expressed as
(kc2 / Ro2) =
H20
( M +
M +

 -
1). The Hubble Constant is thus the key parameter in determining the age
of the universe (with
-
1). The Hubble Constant is thus the key parameter in determining the age
of the universe (with
 M
and
M
and 
 also playing a role). Similarly, physical processes such as the growth
of structure and the nucleosynthesis of light elements (H, D,
3He, 4He, Li), as well as critical epochs in the
Universe's history, such as the transition from a radiation-dominated to
a matter-dominated universe, depend on the cosmic expansion rate and
thereby on the value of H0. It should therefore come
as no surprise that the determination of the value of the Hubble
Constant became a major observational goal for the past eight decades.
also playing a role). Similarly, physical processes such as the growth
of structure and the nucleosynthesis of light elements (H, D,
3He, 4He, Li), as well as critical epochs in the
Universe's history, such as the transition from a radiation-dominated to
a matter-dominated universe, depend on the cosmic expansion rate and
thereby on the value of H0. It should therefore come
as no surprise that the determination of the value of the Hubble
Constant became a major observational goal for the past eight decades.
The first value for the Hubble Constant may have actually been derived
by Lemaître
(1927),
who, on the basis of Slipher's radial velocity measurements and Hubble's
mean absolute magnitude for galaxies ("nebulae") obtained
H0 = 526 km s-1 Mpc-1. The next
set of values by
Hubble (1929)
and Hubble and Humason (who produced a velocity-distance relation up to
V ~ 20000 km s-1 and obtained H0 =
559 km s-1 Mpc-1 in 1931), were all
around 500 km s-1 Mpc-1, with an
uncertainty stated rather naively as "of the area of ten percent." About
twenty years passed before
Baade (1954)
revised the distance to nearby galaxies, recognizing that Hubble
confused two classes of "standard candles" (Population I Cepheids
and Population II W Virginis stars), thereby reducing the
value of H0 by about a factor two (a revision
suggested also by
Behr 1951).
The value of the Hubble Constant first reached the range of values
accepted today through the work of
Alan Sandage
(1958).
Sandage demonstrated that Hubble mistakenly identified H II regions as
bright stars, and he [Sandage] was able to revise the value further to
H0  75 km s-1
Mpc-1 (recognizing that the uncertainty could still be by a
factor 2).
75 km s-1
Mpc-1 (recognizing that the uncertainty could still be by a
factor 2).
In the three decades that followed, published values of the Hubble Constant varied by about a factor of two between ~ 100 and 50 km s-1 Mpc-1. Table 1, adapted from Trimble (1997), summarizes the early history of the constant.
| When | Who | Numerical value | |
| 1927 | Lemaître | 600 | |
| 1929 | Hubble | 530-513-465 | |
| 1931 | Hubble & Humason | 558 | |
| 1936 | Hubble | 526 | |
| 1946 | Mineur | 330 | |
| 1951 | Behr | 250 | |
| 1952 | Baade, Thackeray | 270 | |
| 1956 | Humas, Mayall & Sandage | 180 | |
| 1958 | Holmberg | 134 | |
| 1958 | Sandage | 150-75-38 | |
| 1959 | McVittie | 227-143 | |
| 1960 | Sersic | 125 | |
| 1960 | van den Bergh | 125 | |
| 1960 | van den Bergh | 125 | |
| 1961 | Ambartsumyan | 140-60 | |
| 1961 | Sandage | 113-85 | |
| 1964 | de Vaucouleurs | 125 | |
| 1968-69 | de Vaucouleurs | 100 | |
| 1969 | van den Bergh | 110-83 | |
| 1968-76 | Sandage & Tammann | 50 | |
| 1972 | Sandage | 55 | |
| 1979 | de Vaucoulers | 100 | |
Generally, since redshifts (and therefore radial velocities) can be determined relatively readily (this is, of course, not true for the most distant or faintest objects), the problem of determining the Hubble Constant has always been a problem of determining accurate astronomical distances. The availability of new instrumentation, and the Hubble Space Telescope in particular, have allowed for a dramatic improvement in distance determinations.