


8.4. The nature of "dark energy"
It is beyond the scope of the present article to discuss dark energy in detail and the reader is referred to the excellent review by Peebles and Ratra (2002). However, since this is arguably the most dramatic discovery involving HST I would like to make a few points.
In general relativity, the stress-energy tensor of the vacuum,
T µ
µ , can be written as
, can be written as
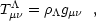 |
(38) |
where 
 is
constant (proportional to Einstein's cosmological constant) and
gµ
is
constant (proportional to Einstein's cosmological constant) and
gµ is
the metric. In a Minkowski flat spacetime this can be written simply as
the "equation of state"
is
the metric. In a Minkowski flat spacetime this can be written simply as
the "equation of state"
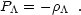 |
(39) |
More generally, if the equation of state is written as (for example, Canuto et al. 1977, Ratra and Peebles 1988, Sahni and Starobinsky 2000, Turner and White 1997),
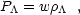 |
(40) |
then the dark energy density behaves (for a constant w) like

 ~
a-3(1+w) (where a is the scale factor). Since
the scale factor satisfies the equation (in units in which c =
1)
~
a-3(1+w) (where a is the scale factor). Since
the scale factor satisfies the equation (in units in which c =
1)
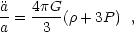 |
(41) |
the dark energy contribution will result in an accelerating universe if w < - 1/3.
It is interesting to note that from a purely fluid dynamical point of
view, any equation of state of the type P = w
 is in fact
dynamically unstable for any negative value of w except
for w = - 1 (corresponding to a cosmological constant). This can
be easily seen from perturbations on the equations for momentum and
energy conservation (<
is in fact
dynamically unstable for any negative value of w except
for w = - 1 (corresponding to a cosmological constant). This can
be easily seen from perturbations on the equations for momentum and
energy conservation (<
 >, <
P > denote mean values)
>, <
P > denote mean values)
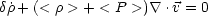 |
(42) |
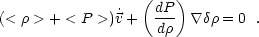 |
(43) |
Defining the speed of sound, c2s = dP /
d , these
two equations can be combined to form
, these
two equations can be combined to form
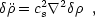 |
(44) |
which is clearly unstable for negative c2s
(except for w = - 1, when the combination
<  > +
< P > vanishes, as expected from the fact that the vacuum
is the same for all inertial observers).
> +
< P > vanishes, as expected from the fact that the vacuum
is the same for all inertial observers).
Thus, formally speaking, from a fluid-dynamical point of view only a cosmological constant yields a stable solution.
One can certainly take the dark energy to be associated with a uniform
scalar field  (a "quintessence" field; see below), that rolls down a potential
V(
(a "quintessence" field; see below), that rolls down a potential
V( ) at a
rate determined by
) at a
rate determined by
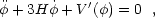 |
(45) |
where V'( ) =
dV /
d
) =
dV /
d . In
this case,
. In
this case,
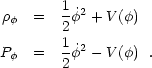 |
(46) |
For a sufficiently slowly varying dynamical component, such that the
kinetic energy is much smaller than the potential,
 2 <<
V(
2 <<
V( ), one
even obtains a field energy that mimics the cosmological constant
(P
), one
even obtains a field energy that mimics the cosmological constant
(P
 -
-

 ). Generally,
quintessence solutions allow for different equations of state, and even
values of w that are time variable. Nevertheless, I find the
stability property expressed in eq. (44) sufficiently intriguing to
warrant a deeper examination of the cosmological constant
possibility, before that is abandoned in favor of other dynamical
solutions. This point of view received some further support from the
recent determination by WMAP that w < - 0.78
(Bennett et
al. 2003).
). Generally,
quintessence solutions allow for different equations of state, and even
values of w that are time variable. Nevertheless, I find the
stability property expressed in eq. (44) sufficiently intriguing to
warrant a deeper examination of the cosmological constant
possibility, before that is abandoned in favor of other dynamical
solutions. This point of view received some further support from the
recent determination by WMAP that w < - 0.78
(Bennett et
al. 2003).
There are two main problems with the implied energy density
 V of
the dark energy (e.g.,
Weinberg 2001).
(i) Why is its value not ~ 120 orders of magnitude larger (as
expected from fluctuations in the gravitational field up to the Planck
scale)? (ii) Why now? (Namely, why
V of
the dark energy (e.g.,
Weinberg 2001).
(i) Why is its value not ~ 120 orders of magnitude larger (as
expected from fluctuations in the gravitational field up to the Planck
scale)? (ii) Why now? (Namely, why

 ~
~
 M now,
even though
M now,
even though 
 may
be associated with a cosmological constant, while
may
be associated with a cosmological constant, while
 M
declined continuously from the initial singularity to its present value).
M
declined continuously from the initial singularity to its present value).
An interesting curiosity to note is that even though taking graviton energies up to Planck scale, MP, misses the value of the dark energy density by ~ 10120, and taking them up to the supersymmetry scale, MSUSY, misses by ~ 1055, a scale of MV ~ (MSUSY / MP)MSUSY actually does give the right order of magnitude! While I am not aware at present of any theory that produces this scale in a natural way (although see, e.g., Arkani-Hamed et al. 2000), I find this coincidence worth following up.
Much of the efforts to resolve the above two problems revolved not around a cosmological constant, but rather around the behavior of quintessence fields. In particular, attention has concentrated on "tracker" solutions, in which the final value of the quintessence energy density is independent of fine-tuning of the initial conditions (e.g., Zlatev, Wang and Steinhardt 1998, Albrecht and Skordis 2000). For example if one takes a potential of the form
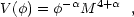 |
(47) |
where  > 0 and
M is an adjustable constant, and the field is initially much
smaller than the Planck mass, then for
> 0 and
M is an adjustable constant, and the field is initially much
smaller than the Planck mass, then for
 M
>>
V(
M
>>
V( ),
),
 2, we find
that
2, we find
that  M
decreases initially faster (~ t-2) than
M
decreases initially faster (~ t-2) than
 (t)(~
t-2
(t)(~
t-2 /
(2+
/
(2+ )).
)).
Eventually, however, a transition to a

 -dominated
universe occurs (and
-dominated
universe occurs (and

 decreases as
t-2 /
(4+
decreases as
t-2 /
(4+ )). In other
words, the quintessence answer to the question: why is the dark energy
density so small? is simply: because the universe is very
old. Nevertheless, simple potentials of the form (47) do not offer a
clear solution to the "why now?" problem. In fact, to have
)). In other
words, the quintessence answer to the question: why is the dark energy
density so small? is simply: because the universe is very
old. Nevertheless, simple potentials of the form (47) do not offer a
clear solution to the "why now?" problem. In fact, to have

 ~
~
 M
(and of order of the critical density) at the present time requires
fine-tuning the parameters so that (for example,
Weinberg 2001)
M
(and of order of the critical density) at the present time requires
fine-tuning the parameters so that (for example,
Weinberg 2001)
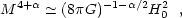 |
(48) |
with no simple explanation as to why this equality should hold.
In order to overcome this requirement for fine-tuning, some versions of the quintessence models choose potentials in which the universe has periodically been accelerating in the past (the dark energy has periodically dominated the energy density; e.g., Dodelson, Koplinghat & Stewart 2000). Dodelson et al. 2000 have shown, for example, that with a potential of the form
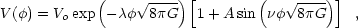 |
(49) |
one can obtain solutions in which the dark energy density tracks the ambient energy density of the universe and satisfies observational constraints.
A different approach to the problems associated with the dark energy
density has been through anthropic considerations (e.g.,
Weinberg 2001,
Vilenkin 1995,
Kallosh and Linde
2002).
The key assumption in this class of models is that some constants
of nature, in particular the cosmological constant, and possibly the
density contrast at the time of recombination,
 rec, are in
fact random variables, whose range of values and a priori
probabilities are nevertheless determined by the laws of physics. In
this picture, some values of the constants which are allowed in
principle, may be incompatible with the very existence of
observers. Assuming a principle of mediocrity - that we should
expect to find ourselves in a universe typical of those that
allow the emergence of intelligent life -
Garriga, Livio
and Vilenkin (2000)
were able to show that the "why so small?" and "why now?" questions find
a natural explanation. While I personally believe that anthropic
considerations should only be used as a last resort, there is no denial
of the fact that most versions of "eternal inflation," the notion that
once inflation starts it never stops, unavoidably produce an ensemble of
"pocket" universes
(Guth 1981,
Vilenkin 1983,
Linde 1986,
Steinhardt
1983).
Once such an infinite ensemble is believed to exist, the problem of
defining probabilities on it, and the concept of "mediocrity" become
real (e.g.,
Linde, Linde and
Mezhlumian 1995,
Vilenkin 1998).
rec, are in
fact random variables, whose range of values and a priori
probabilities are nevertheless determined by the laws of physics. In
this picture, some values of the constants which are allowed in
principle, may be incompatible with the very existence of
observers. Assuming a principle of mediocrity - that we should
expect to find ourselves in a universe typical of those that
allow the emergence of intelligent life -
Garriga, Livio
and Vilenkin (2000)
were able to show that the "why so small?" and "why now?" questions find
a natural explanation. While I personally believe that anthropic
considerations should only be used as a last resort, there is no denial
of the fact that most versions of "eternal inflation," the notion that
once inflation starts it never stops, unavoidably produce an ensemble of
"pocket" universes
(Guth 1981,
Vilenkin 1983,
Linde 1986,
Steinhardt
1983).
Once such an infinite ensemble is believed to exist, the problem of
defining probabilities on it, and the concept of "mediocrity" become
real (e.g.,
Linde, Linde and
Mezhlumian 1995,
Vilenkin 1998).
In spite of the apparent "success" of the anthropic argumentation in solving the two main problems associated with dark energy, the search for a fundamental explanation is not, and should not, be abandoned. An interesting, if speculative, new direction is provided by alternative theories of gravity. For example, models in which ordinary particles are localized on a three-dimensional surface (3-brane) embedded in infinite volume extradimensions to which gravity can spread, have been developed (Deffayet, Dvali, and Gabadadze 2002). In a particular version of these models, the Friedmann equation (eq. 24) is replaced by
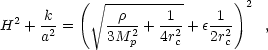 |
(50) |
where  = ± 1,
and rc represents a crossover scale. At distances
shorter than rc (which can be of astronomical size,
e.g., rc ~ cH0-1),
observers on the brane discover the familiar Newtonian gravity. At large
cosmological distances, however, the force-law of gravity becomes
five-dimensional (as gravity spreads into the extra dimensions) and
weaker. The dynamics are governed by whether
= ± 1,
and rc represents a crossover scale. At distances
shorter than rc (which can be of astronomical size,
e.g., rc ~ cH0-1),
observers on the brane discover the familiar Newtonian gravity. At large
cosmological distances, however, the force-law of gravity becomes
five-dimensional (as gravity spreads into the extra dimensions) and
weaker. The dynamics are governed by whether
 /
Mp2 is larger or smaller than 1 /
rc2. While highly speculative at this
stage, some aspects of these alternative theories of gravity can be
experimentally tested (e.g., by lunar ranging experiments;
Dvali, Gruzinov and
Zaldarriaga 2002).
Also, the relative lack of power on large scales (in particular, absence
of any correlated signal on scales larger than 60 degrees) found by
the Wilkinson Microwave Anisotropy Probe
(Spergel et
al. 2003),
may indicate a breakdown of canonical gravity on large scales (or, more
speculatively, a finite universe).
/
Mp2 is larger or smaller than 1 /
rc2. While highly speculative at this
stage, some aspects of these alternative theories of gravity can be
experimentally tested (e.g., by lunar ranging experiments;
Dvali, Gruzinov and
Zaldarriaga 2002).
Also, the relative lack of power on large scales (in particular, absence
of any correlated signal on scales larger than 60 degrees) found by
the Wilkinson Microwave Anisotropy Probe
(Spergel et
al. 2003),
may indicate a breakdown of canonical gravity on large scales (or, more
speculatively, a finite universe).
Luckily, observations that are already being performed with HST, and observations with the proposed Super Nova/Acceleration Probe (SNAP) will provide some crucial information on the nature of dark energy. In particular, if the equation of state parameter w is constant, then a transition from a decelerating phase to an accelerating phase occurs at
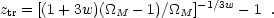 |
(51) |
For example, for
 M = 0.27
(Bennett et
al. 2003)
and a cosmological constant (w = - 1), this gives
ztr
M = 0.27
(Bennett et
al. 2003)
and a cosmological constant (w = - 1), this gives
ztr  0.76. Equation (51) shows that if
0.76. Equation (51) shows that if
 M can be
determined independently to within a few percent (a goal that can
perhaps be achieved by a conbination of cosmic microwave background and
large scale structure measurements), then observations of a large sample
of Type Ia supernovae in the redshift range 0.8-2 can place very
meaningful constraints on the dark energy equation of state. The
situation is more ambiguous if w is time-dependent, but even
then, a sufficiently large sample of SNe Ia will give useful
information. At the time of this writing, a search for SNe Ia
conducted in the GOODS fields has already yielded 10 SNe Ia,
with six of them in the redshift range z ~ 1-2 (Principal
Investigator: Adam Riess). This, together with a few current
ground-based searches at lower redshifts, is an excellent first
step. The survey proposed by SNAP, of 15 square degrees, could
yield light curves and spectra for over 2000 SNe Ia at redshifts up
to z ~ 1.7. With this sample in hand, one could reach the
elimination or at least control of the sources of systematic
uncertainties needed to discriminate between different dark-energy models.
M can be
determined independently to within a few percent (a goal that can
perhaps be achieved by a conbination of cosmic microwave background and
large scale structure measurements), then observations of a large sample
of Type Ia supernovae in the redshift range 0.8-2 can place very
meaningful constraints on the dark energy equation of state. The
situation is more ambiguous if w is time-dependent, but even
then, a sufficiently large sample of SNe Ia will give useful
information. At the time of this writing, a search for SNe Ia
conducted in the GOODS fields has already yielded 10 SNe Ia,
with six of them in the redshift range z ~ 1-2 (Principal
Investigator: Adam Riess). This, together with a few current
ground-based searches at lower redshifts, is an excellent first
step. The survey proposed by SNAP, of 15 square degrees, could
yield light curves and spectra for over 2000 SNe Ia at redshifts up
to z ~ 1.7. With this sample in hand, one could reach the
elimination or at least control of the sources of systematic
uncertainties needed to discriminate between different dark-energy models.