Copyright © 1997 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 1997. 35:
503-556 Copyright © 1997 by Annual Reviews. All rights reserved |
The existence of an age-metallicity relation (AMR) in the disk is an important issue for developing chemical evolution models. There is currently some uncertainty whether an AMR exists: Studies of open cluster metallicities and ages (e.g. Arp 1962, Geisler 1987, Geisler et al 1992, Friel & Janes 1993) have resulted in the conclusion by some that there is no AMR in the Galactic disk (see the review by Friel 1995). The main factor in determining open cluster metallicity appears to be galactocentric radius (e.g. Geisler et al 1992). It is also clear that there is a large scatter in metallicity at any given age in the disk: The dispersion in the age-metallicity diagram is exemplified by the presence of very old open clusters with metallicities near or above the solar value. The open cluster NGC 188 has historically been used to illustrate this point (e.g. Eggen & Sandage 1969); but the most clear-cut modern case is NGC 6791, which is more metal-rich than the sun, with [Fe/H] ~ +0.2 to +0.3 dex (Peterson & Green 1995, Montgomery et al 1994), but very old at ~ 10 × 109 years (Montgomery et al 1994, Tripicco et al 1995).
The conclusion against an AMR is at odds with claims based on studies of
field stars. For example,
Twarog (1980),
Meusinger et al
(1991),
Jønch-Sørensen
(1995) all employed
uvby
photometry
and found a trend of decreasing metallicity with increasing stellar age.
Edvardsson et al
(1993)
used spectroscopic abundance analysis to determine [Fe/H] and
uvby
photometry for the ages. They found an AMR consistent with the results of
Twarog (1980),
Meusinger et al
(1991)
but with a considerable scatter about the mean trend
(Figure 2).
The Jønch-Sørensen data indicated a similar AMR slope and
scatter as Edvardsson
et al's data. The age-metallicity diagram from these studies (e.g.
Figure 2)
show a lower envelope to the observed metallicity of stars that increases
with Galactic time; in particular, no young stars with [Fe/H] ~
-1 have been found in the solar neighborhood (although low metallicity
stars at large galactocentric radii are known; e.g.
Geisler 1987,
Geisler et al 1992).
 |
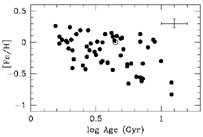Figure 2. The age-metallicity relation for
the solar neighborhood, from the data of
Edvardsson et al
(1993).
The sample is limited to galactocentric radius 7.7
|
The large scatter in metallicity at all ages is the one consistent conclusion common to the age-metallicity diagrams for both the field stars and open clusters. François & Matteucci (1993) suggested that the scatter could be due to orbital diffusion; however, Edvardsson et al (1993) showed that this is not enough to reduce the observed scatter in the age-metallicity diagram.
It is clear that certain biases occur in samples of field stars that could conspire to create an apparent AMR, even if none exists (Knude 1990, Grenon 1987); indeed, Friel (1995) states that the age-metallicity trends seen by Twarog (1980) are the result of these selection effects. However, Twarog was aware of the selection biases and pointedly went to great effort to avoid them. Jønch-Sørensen (1995) estimated an upper limit to the number of metal-poor young stars and claimed that the selection bias against metal-poor young stars could not account for the apparent AMR. Edvardsson et al (1993) made a correction for a metallicity bias, but the AMR was still present. Obviously a definitive resolution to the existence or absence of a mean AMR in field stars would be extremely valuable. If age and metallicity data for the halo are added to Figure 2, as done by Eggen & Sandage (1969), a strong AMR would result; however, the validity of combining these two populations is not certain.
The large range of metallicities present for all ages suggests that chemical enrichment up to solar metallicity can occur on rapid time scales (~ 1 × 109 years) and that the disk has been chemically inhomogeneous throughout its development. The dispersion in the AMR at the solar circle (as seen in the Edvardsson et al 1993 study) shows that the composition of the Galactic disk did not evolve homogeneously. Traditional chemical evolution models, for example those of Lynden-Bell (1975), Larson (1976), Matteucci & François (1989), Pagel (1989), Sommer-Larsen (1991), Pagel & Tautvaisiene (1995), cannot account for the observed AMR dispersion because they all assume instantaneous mixing of recycled gas and a homogeneous steady infall; as a consequence chemical homogeneity is preserved at all times.
Reeves (1972) suggested that significant spatial inhomogeneities in elemental abundances could occur as a result of self-enrichment of star-forming regions by SN events. However, Edmunds (1975) investigated this possibility and concluded that the Galactic disk is well mixed. White & Audouze (1983) developed analytical expressions that extended the standard chemical evolution model of Lynden-Bell (1975) to the case of inhomogeneous steady-state evolution. Two important mixing parameters dictated the inhomogeneity: (a) the mean mass of disk material mixed with a unit mass of enriched material from star formation events and (b) the mean mass of disk material mixed with a unit mass of infalling gas.
Recent models of Galactic evolution attempted to describe inhomogeneous chemical evolution: (Pilyugin & Edmunds 1996a, b Raiteri et al (1996). Both studies adopt the Twarog (1980) AMR and the dispersion about this relation indicated by Edvardsson et al (1993).
Pilyugin & Edmunds (1996b) considered inhomogeneity by two mechanisms. In the first approach, self-enrichment of gas in star forming regions (H II regions) for 3 × 107 years is permitted, after which time the gas is instantaneously mixed with the ambient disk gas. This approximates a star-forming region in which SN ejecta enrich the region with metals until the energy input from SN is sufficient to disrupt the cloud in 3 × 107 years, followed by mixing with the disk in ~ 108 years. Justification for this assumption comes from (Cunha & Lambert 1992, 1994), who showed that self enrichment in the Orion association has occurred in ~ 80 × 106 years, based on enhancements in O and Si abundances as a function of age of the Orion subgroups.
Self enrichment of the H II regions gave a satisfactory fit to the dispersion in the oxygen abundance with time, but it was incapable of reproducing the observed dispersion in Fe abundance. The difficulty in reproducing the Fe dispersion was caused by the fact that Fe is produced mainly in SN Ia, whose progenitor lifetimes are thought to be ~ 1 × 109 years, well in excess of the self-enrichment time scale. Pilyugin & Edmunds (1996b) suggest that self-enrichment of H II regions results in larger dispersion for oxygen abundances SN II progenitors with short lifetimes) than iron abundances versus age. They concluded that the large observed dispersion for both O and Fe implicates another source of inhomogeneity.
Pilyugin & Edmunds (1996b) suggested that episodic gas infall could account for the large dispersions in the AMR for both Fe and O. If infalling gas fell onto the disk in a nonuniform fashion both temporally and spatially), then disk gas could reach solar metallicity followed by substantial dilution to lower metallicities. Stars formed over such a cycle would exhibit equal Fe and O dispersion in the AMR because dilution affects all species equally. If this is the case, then the infalling gas cannot be pure hydrogen; otherwise the dilution would preserve solar abundance ratios even near [Fe/H] = -1, which is not observed. The gas would need to be of halo composition, with [Fe/H] ~ -1, to avoid the problem of solar ratios in low metallicity disk stars.
Raiteri et al (1996) have developed N-body/hydrodynamical simulations of Galactic chemical evolution. The method seems very promising and does produce an AMR similar to Twarog' (1980) with a large metallicity dispersion; it also predicts significant dispersion in the [O/Fe] ratio at all metallicities, which provides a basis for testing the model. There are some problems, however, such as a very high frequency of low metallicity stars.
Rm