Annu. Rev. Astron. Astrophys. 1997. 35: 503-556 Copyright © 1997 by Annual Reviews. All rights reserved

8.1. Disk and Bulge Heavy Elements

The notion that most heavy elements scale with [Fe/H] in the disk has been known for some time (e.g. Wallerstein 1962, Helfer & Wallerstein 1968, Pagel 1968, Huggins & Williams 1974, Butcher 1975). The most accurate and largest samples of disk dwarf abundances are the studies of Edvardsson et al (1993), Woolf et al (1995); also McWilliam (1990) presented abundance results for a large number of disk giants.

The Edvardsson et al results demonstrate that the abundance of Y in the first s-process peak, and Ba and Nd in the second s-process peak, scale with metallicity down to [Fe/H] = -1. This observation is apparently at odds with the picture of primary and secondary elements: The s-process elements are made by the addition of neutrons to preexisting iron seed nuclei. Thus, the [s-process/Fe] abundance ratios are expected to behave like secondary elements, proportional to [Fe/H], rather than independent of the metallicity, as is observed. Clayton (1988) proposed that s-process abundances scale with metallicity if they were produced by the ¹³C(, n)¹⁶O neutron source in AGB stars; also, the increased neutron fluence in the model led to the prediction of increased [Ba/Y] ratios at low metallicity. This prediction was supported by the observed high [Ba/Y] abundance ratios found for CH stars (Vanture 1992, 1993) and Cen giants (e.g. Vanture et al 1994) and the abundance ratios in S and MS stars (see Busso et al 1995).

The metallicity dependence of the [Ba/Y] ratio produced in the s-process leads to a puzzle: If AGB stars are the source of the s-process elements in the disk, then why is the observed [Ba/Y] ratio approximately ~ 0.0 dex over the full metallicity range of disk stars?

Part of the answer must be due to the transition from halo-like composition ([Ba/Y] = +0.06) gas near [Fe/H] = -1 to solar composition at [Fe/H] = 0.0; both have similar [Ba/Y] values. Perhaps a more important factor is the presence of a large metallicity dispersion in the disk over most of Galactic history. In particular, the inhomogeneous chemical evolution models of White & Audouze (1983) showed that when there is a large dispersion in metallicity, the slopes for secondary elements can be erased; this is because at any given time the secondary elements were produced in sources with a large range of metallicity. Thus, the metallicity dispersion ensured that the [Ba/Y] ratio in the disk was always close to the average value.

Woolf et al (1995) measured [Eu/Fe] ratios in solar neighborhood F and G stars with -0.9 [Fe/H] +0.3. Their results showed increasing [Eu/Fe] ratios with decreasing [Fe/H]; this trend was also reported by McWilliam & Rich (1994), although there was some considerable scatter about the mean relation. The [Eu/Fe] ratios match the trend of increasing -element abundances with [Fe/H]; from the [Eu/Fe] trends in the disk and the halo, one would classify Eu as an element. Because Eu is a nearly pure r-process element, the observed trend with metallicity is consistent with the notion that the r-process and elements are made in SN II see Figure 8). For stars more metal-rich than the Sun, Woolf et al (1995) found subsolar [Eu/Fe] ratios, unlike the [ / Fe] ratios that remain at the solar value above solar metallicity. The idea proposed by Maeder (1991) to explain the trend of [O/Fe] with [Fe/H] as due to the onset of Wolf-Rayet stars would have to affect the [Eu/Fe] ratio in the same way as the [O/Fe] ratios. It is difficult to imagine how such a process might occur in current models of SN II, which holds that Eu is formed during the SN II event, deep inside the exploding star, whereas the ejected O is produced in higher regions of the star during the hydrostatic burning phase.

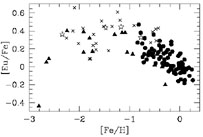Figure 8. The run of the (almost) pure r-process element europium with metallicity for field stars; indicated by filled circles for the disk (Woolf et al 1995) and in the halo by crosses (Shetrone 1996a) and filled triangles (Gratton & Sneden 1994). The open stars indicate mean values for the globular clusters M71, M13, M5, and M92 from (Shetrone 1996a).

The Zr results from Edvardsson et al (1993) show a trend towards enhanced [Zr/Fe], reaching +0.2 dex in the lower metallicity disk stars; given the enhanced [Zr/Fe] ratios in the halo stars (Magain 1989, Gratton & Sneden 1994), this may suggest that SN II produce significant amounts of Zr.

Edvardsson et al (1993) showed that in the disk, [Ba/Fe] ratios increased with time and were very roughly independent of metallicity; from log age 0.9 to < 0.6 Gyr, the mean [Ba/Fe] ratio increased from -0.1 to +0.1 dex. The halo fits into this picture, with a mean [Ba/Fe] ratio of ~ -0.1 dex (Gratton & Sneden 1994). This trend in [Ba/Fe] suggests that there is a source that produced Ba on a time scale longer than the time scale for Fe production. This conclusion is consistent with the idea that s-process nucleosynthesis is dominated by AGB stars over the mass range 1-3 M (Meyer 1994) or 1-4 M (Busso et al 1995). The steady increase in the disk [Ba/Fe] ratio with Galactic time is probably due to the delay in Ba production from the lower mass stars in this range, say 1-2 M, with main-sequence lifetimes of several billion years.

The results of Edvardsson et al (1993) show a steeper slope for [Ba/H] with age than [Fe/H] with age; also, despite the larger measurement uncertainties for Ba, the age-[Ba/H] relation shows less dispersion than the age-[Fe/H] relation. The steep slope of [Ba/H] with age must be due in part to the gradual increase in [Ba/Fe] with time due to the long-lived sources. If the intrinsic dispersion in the age-[Ba/H] relation is actually significantly smaller than for the age-[Fe/H] relation, then this must be understood in the context of disk chemical evolution models that describe the dispersion in the age-metallicity relation (e.g. Pilyugin & Edmunds 1996b). A characteristic of the Pilyugin & Edmunds (1996b) model is that it predicts roughly equal dispersion for all elements.

The fact that the [Ba/Fe] ratio is sensitive to age might have applications for other locations, such as the Galactic bulge. For the bulge, McWilliam & Rich (1994) found the mean [s-process/iron] ratio of ~ 0.0 dex, from lines of Y, La, and Ba. In particular, a subsolar value of [s-process/Fe] near -0.1 dex, expected if the bulge formation time scale was rapid, is inconsistent with the data. Certainly more accurate and extensive measurements of s-process elements in the bulge are necessary to verify this point.