Probing the Universe with Weak Lensing

Annu. Rev. Astron. Astrophys. 1999. 37: 127-189
Copyright © 1999 by Annual Reviews. All rights reserved

2.2. Relation with Observable Quantities

Let us assume that, to first approximation, faint galaxies can be described as ellipses. Their shape can be expressed as a function of their weighted second moments which fully define the properties of an ellipse,

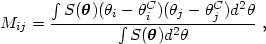$\begin{equation} M_{ij}= {\int S(\thetag) (\theta_i-\theta^C_i)(\theta_j-\theta^C_j) d^2\theta \over \int S(\thetag) d^2\theta } \ , \end{equation}$

(9)

where the subscripts ij denote the axes (1, 2) of coordinates theta in the source and the image planes, S( theta ) is the surface brightness of the source and theta ^C is the center of the source.

Since the surface brightness of the source is conserved through the gravitational lensing effect (Etherington 1933), it is easy to show that, if one assumes that the magnification matrix is constant across the image (lensed source), the relation between the shape of the source, M^S and the lensed image, M^I is

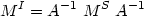$\begin{equation} M^I=A^{-1} \ M^S \ A^{-1} \end{equation}$

(10)

Therefore, to first approximation, the gravitational lensing effect on a circular source changes its size (magnification) and transforms it into an ellipse (distortion) with axis ratio given by the ratio of the two eigenvalues of the magnification matrix. The shape of the lensed galaxies can then provide information about these quantities. The approximation that the magnification matrix is constant over the image area is always valid in the weak-lensing regime, because the spatial scale variation of the magnification is much larger than the typical size of the lensed galaxies (a few arcseconds). This is not the case when the magnification tends to infinity, but this case is beyond the scope of this review (see Schneider et al 1992, Fort & Mellier 1994).

The relation between the lens quantities described in Section 2.1 and the shape parameters of lensed galaxies is not immediately apparent. Although gamma ₁ and gamma ₂ describe the anisotropic distortion of the magnification, they are not directly related to observables (except in the weak-shear regime). 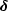It is preferable to use the reduced complex shear, g, and the complex polarization (or distortion), delta , which is an observable,

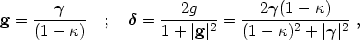$\begin{equation} \boldg={\gammag \over (1-\kappa)} \ \ \ ; \ \ \ \deltag= { 2 g \over 1 + \vert \boldg\vert^2} ={2 \gammag (1-\kappa) \over (1-\kappa)^2+\vert \gammag \vert^2} \ , \end{equation}$

(11)

because 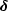delta can be expressed in terms of the observed major and minor axes a^I and b^I of the image, I, produced by a circular source S:

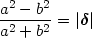$\begin{equation} { a^2 - b^2 \over a^2 +b^2} = \vert \deltag \vert \end{equation}$

(12)

In this case, the two components of the complex polarization are easily expressed with the second moments:

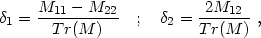$\begin{equation} \delta_1={M_{11}-M_{22} \over Tr(M)} \ \ \ ; \ \ \ \delta_2={ 2 M_{12} \over Tr(M)} \ , \end{equation}$

(13)

where Tr(M) is the trace of the magnification matrix. For non-circular sources, from Equations (8) and (11) it is possible to relate the ellipticity of the image epsilon ^I to the ellipticity of the lensed source, epsilon ^S. In the general case, it depends on the sign of Det (A) (that is the position of the source with respect to the caustic lines) which expresses whether images are radially or tangentially elongated. In most cases of interest, Det(A) > 0 (the external regions, where the weak lensing regime applies) and:

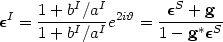$\begin{equation} \epsilong^I={1 + b^I / a^I \over 1 + b^I / a^I} e^{2 i \vartheta} = {\epsilong^S + \boldg \over 1 - \boldg^* \epsilong^S} \end{equation}$

(14)

(Seitz & Schneider 1996), but when Det(A) > 0:

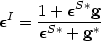$\begin{equation} \epsilong^I= {1+ \epsilong^{S*} \boldg \over \epsilong^{S*} + \boldg^*} \end{equation}$

(15)

Equations 14 and 15 summarize most of the cases that will be discussed in this review.