Annu. Rev. Astron. Astrophys. 1999. 37: 127-189 Copyright © 1999 by Annual Reviews. All rights reserved

7.1. Constraints from Cluster Reconstruction

Following the early suggestion by Paczynski & Gorski (1981) for multiply imaged quasars, Breimer & Sanders (1992) (see also Fort & Mellier 1994, Link & Pierce 1998) emphasized that the ratio of angular diameter distances of arc(let)s having different redshifts does not depend on the Hubble constant and therefore can constrain (, ). This ratio still depends on the mass distribution within the two critical lines corresponding to redshifts z₁ and z₂, so it is worth noting that it is sensitive to the modeling of the lens. It is only in the case of an isothermal sphere model that the radial positions of the critical lines , where arcs at a given redshift are formed, only depend on the angular distances D(z_s, ₀, ):

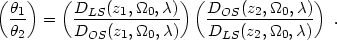(40)

Because cluster potentials are by far more complex than isothermal spheres, in practice the method works only for very specific cases, such as clusters with regular morphology, and if auxiliary independent data, such as high-quality X-ray images or additional multiple images, help to constrain the lens model. So far, no case has been found where the modeling of two (or more) arc systems at very different redshifts is sufficiently reliable. However, the joint HST images and spectroscopic redshifts obtained with new giant telescopes should provide such perfect configurations in the near future. A1689 or MS0440 seem like good examples of such candidates because both show many arc(let)s and have a regular shape.

A similar approach has been proposed by Hamana et al (1997), using the arc cB58 observed in the lensing cluster MS1512.4+3647. Assuming that the dark matter distribution is sufficiently constrained by the ROSAT and ASCA data, the magnification and number of multiple images of cB58 only depend on the cosmology. One should therefore use the detection of counter-image to cB58 to constrain the domain (₀, ) which cannot produce a counter-arc. This point was discussed by Seitz et al (1997) who argue that in practice it cannot work because it depends too much on the modeling of the lensing cluster. The variation of the lensing strength as a function of cosmology is small, lower than 0.5% between an EdS universe and an = 0.3, = 0 universe. Furthermore, the use of independent X-ray data to model the dark matter demands a very good understanding of the physics of the hot gas for each individual cluster considered.

More recently, Lombardi & Bertin (1999) have proposed the use of weak lensing inversion to recover simultaneously the cluster mass distribution and the geometry of the universe. The method assumes that the redshifts of the lensed galaxies are known. In that case, for a given cosmology, it is possible to compute the shear at a given angular position which is produced on a lensed galaxy located in a narrow redshift range, from the observed ellipticities of the galaxies at that angular position. Conversely, if the shear is known, then it is possible to infer the best set of cosmological parameters which reproduce the observed ellipticities of the galaxies. Therefore, it is possible to iterate a procedure, starting from an arbitrary guess for the set (, ), which at the final step will simultaneously procure the best mass inversion with the most probable (, ). The key point is the assumption that the redshift of each individual source is known. The method should provide significant results if at least a dozen of clusters with different redshift are reconstructed using this iterative procedure (Lombardi & Bertin 1999). Indeed, this inversion is demanding in telescope time since a very good knowledge of the redshifts of many lensed sources is necessary; but otherwise the method seems promising.