Copyright © 1999 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 1999. 37:
409-443 Copyright © 1999 by Annual Reviews. All rights reserved |
4.2. A Relativistic Distance Determination
We note that the detection of a known line from either
of the condensations would allow a precise determination of the distance.
The Doppler factors, namely, the ratios of observed to emitted frequency
(
0) for the
approaching and receding condensations are given by
 |
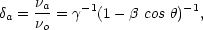(6) |
 |
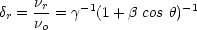(7) |
In these last two equations
= (1 -
2)1/2 is the Lorentz factor. Since we
know cos
, a determination of
either
a /
0
or r /
0
will allow the determination of
and thus the
determination of
and of the distance from Equation (4). In the case of cosmologically distant
objects, the Equations 1, 2, 4, and 5 are valid replacing the distance
D by the angular size distance Da
(Peebles 1993),
and the rest frequency 0 by
0 / (1 + z),
with z being the observed redshift of the central source. The
angular size distance is given by Da = (cz /
H0)[1 - (1 + q0)z / 2 + ...], where
H0 is Hubble's constant and q0 is
the dimensionless acceleration (or deceleration) parameter.
Then, the observations of proper motions and frequency shifts in
extragalactic relativistic ejecta pairs could potentially be used to
test between different cosmological models.