


2.2. Statistical properties of H II regions
Statistical properties of H II region populations offer important quantitative characterizations of global star formation in galaxies. The H II region luminosity function (H II LF) reveals the relative importance of major star-forming events, hosting super star clusters, and smaller, ordinary OB associations. The H II LF has been determined for many nearby galaxies, including all of the star-forming galaxies in the Local Group (Milky Way: Smith & Kennicutt 1989, McKee & Williams 1997; Magellanic Clouds, M31, M33: Kennicutt et al. 1989, Walterbos & Braun 1992, Hodge et al. 1999; IC 10, Leo A, Sex A, Sex B, GR8, Peg, WLM: Youngblood & Hunter 1999). There is agreement that the H II LF universally appears to be described by a power law:
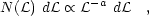 |
(2.5) |
with a power-law index a ~ 2 for the differential LF.
Figure 1 presents Monte Carlo models by
Oey & Clarke (1998a)
that show the existence of a flatter slope below log
 ~ 37.5 - 38.5, owing to a
transition
at low luminosity to objects dominated by small number statistics in
the ionizing stellar population. We also see that
the H II LF can offer some insights on the
nature and history
of the very most recent global star formation, within the last ~ 10 Myr.
~ 37.5 - 38.5, owing to a
transition
at low luminosity to objects dominated by small number statistics in
the ionizing stellar population. We also see that
the H II LF can offer some insights on the
nature and history
of the very most recent global star formation, within the last ~ 10 Myr.
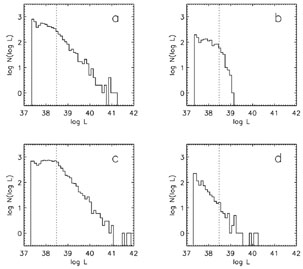 |
Figure 1. Monte Carlo models of the
H II LF from
Oey & Clarke (1998a):
(a) constant nebular creation rate for a full power law in
N* given by equation 6; (b) continuous
creation with an upper cutoff in N* of 10
ionizing
stars; (c) zero-age instantaneous burst for all objects, with a
full power law in N*;
(d) the evolved burst in (c) after 7 Myr. The maximum stellar
ionizing luminosity in the IMF here corresponds to log
|
The observed behavior of the H II LF is consistent with the existence of a universal power law for the number of ionizing stars N* per cluster (Oey & Clarke 1998a):
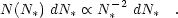 |
(2.6) |
This is consistent with direct observations of the cluster luminosity and mass functions in a variety of regimes (see Chandar, this volume; Elmegreen & Efremov 1997; Meurer et al. 1995; Harris & Pudritz 1994). Such a universal power-law for the cluster mass function is fundamental, similar to the stellar initial mass function (IMF; e.g., Oey & Muñoz-Tuñon 2003).
The nebular size distribution has also been determined in many galaxies, although it has been studied in less detail than the H II LF (Milky Way, Magellanic Clouds, M31, M33, NGC 6822: van den Bergh 1981, Hodge et al. 1999; IC 10, Leo A, Sex A, Sex B, GR8, Peg, WLM: Hodge 1983, Youngblood & Hunter 1999). In his pioneering work, van den Bergh (1981) described the size distribution as an exponential:
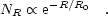 |
(2.7) |
However, this relation is difficult to reconcile with the power-law
form of the H II LF. To first order, the
H
With a slope also flattening below a value of log R ~ 130 pc,
corresponding to the transition in the H II
LF above, this form of the
size distribution is also a good description of the available data
(Oey et al. 2003).
Our initial investigation shows good agreement
between observations and the predicted value for b = 4,
implied by the H II LF slope a = 2.
 luminosity
luminosity
 should scale with the
volume emission as R3, and thus the size distribution
should have a
similar power-law form to that of the H II
LF, but with exponent
b = 2 - 3a. We can see in
a and c that the
existence of the turnover in the H II LF
described above can cause
the entire H II LF to mimic an exponential
form. Thus we suggest that the intrinsic form of the size distribution
is also a power-law relation:
should scale with the
volume emission as R3, and thus the size distribution
should have a
similar power-law form to that of the H II
LF, but with exponent
b = 2 - 3a. We can see in
a and c that the
existence of the turnover in the H II LF
described above can cause
the entire H II LF to mimic an exponential
form. Thus we suggest that the intrinsic form of the size distribution
is also a power-law relation:
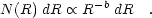
(2.8)