


2.1. Type II Supernovae and the Expanding Photosphere Method
Massive stars come in a wide variety of luminosities and sizes and would seemingly not be useful objects for making distance measurements under the standard candle assumption. However, from a radiative transfer standpoint these objects are relatively simple and can be modeled with sufficient accuracy to measure distances to approximately 10%. The expanding photosphere method (EPM), was developed by Kirshner and Kwan [44], and implemented on a large number of objects by Schmidt et al. [86] after considerable improvement in the theoretical understanding of type II SN (SNII) atmospheres [15, 16, 99].
EPM assumes that SNII radiate as dilute blackbodies
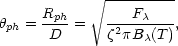 |
(1) |
where  ph is the
angular size of the photosphere of the SN,
Rph is the radius
of the photosphere, D is the distance to the SN,
F
ph is the
angular size of the photosphere of the SN,
Rph is the radius
of the photosphere, D is the distance to the SN,
F is the observed flux density of the SN, and
B
is the observed flux density of the SN, and
B (T) is the Planck function at a
temperature T. Since SNII are not perfect blackbodies, we
include a correction factor,
(T) is the Planck function at a
temperature T. Since SNII are not perfect blackbodies, we
include a correction factor,
 , which is
calculated from radiate transfer models of SNII. SNe freely expand, and
, which is
calculated from radiate transfer models of SNII. SNe freely expand, and
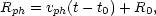 |
(2) |
where vph is the observed velocity of material at the position of the photosphere, and t is the time elapsed since the time of explosion, t0. For most stars, the stellar radius, R0, at the time of explosion is negligible, and Eqs. (1-2) can be combined to yield
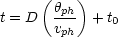 |
(3) |
By observing a SNII at several epochs, measuring the flux density
and temperature of the SN (via broad band
photometry) and vph from the minima of the weakest
lines in the SN spectrum, we can solve simultaneously for
the time of explosion and distance to the SNII. The key to
successfully measuring distances via EPM is
an accurate calculation of
 (T).
Requisite calculations were performed by Eastman et al.
[16]
but, unfortunately, no other calculations of
(T).
Requisite calculations were performed by Eastman et al.
[16]
but, unfortunately, no other calculations of
 (T)
have yet been published for typical SNIIP progenitors.
(T)
have yet been published for typical SNIIP progenitors.
Hamuy et al. [34] and Leonard et al. [52] have measured the distances to SN1999em, and they have investigated other aspects of EPM. Hamuy et al. [34] challenged the prescription of measuring velocities from the minima of weak lines and developed a framework of cross correlating spectra with synthesized spectra to estimate the velocity of material at the photosphere. This different prescription does lead to small systematic differences in estimated velocity using weak lines but, provided the modeled spectra are good representations of real objects, this method should be more correct. At present, a revision of the EPM distance scale using this method of estimating vph has not been made.
Leonard et al.
[51]
have obtained spectropolarimetry of SN1999em at many epochs
and see polarization intrinsic to the SN which is consistent with the SN
have asymmetries of 10 - 20%.
Asymmetries at this level are found in most SNII
[101],
and may ultimately limit the
accuracy EPM can achieve on a single object
( ~ 10%).
However, the mean of all SNII distances should remain unbiased.
~ 10%).
However, the mean of all SNII distances should remain unbiased.
Type II SNe have played an important role in measuring the Hubble constant independent of the rest of the extragalactic distance scale. In the next decade it is quite likely that surveys will begin to turn up significant numbers of these objects at z ~ 0.5 and, therefore, the possibility exists that SNII will be able to make a contribution to the measurement of cosmological parameters beyond the Hubble Constant. Since SNII do not have the precision of the SNIa (next section) and are significantly harder to measure, they will not replace the SNIa but will remain an independent class of objects which have the potential to confirm the interesting results that have emerged from the SNIa studies.