


5.2. Obstacles to Measuring Luminosity Distances at High-Z
As shown above, the distances measured to SNIa are well characterized at z < 0.1, but comparing these objects to their more distant counterparts requires great care. Selection effects can introduce systematic errors as a function of redshift, as can uncertain K-corrections and a possible evolution of the SNIa progenitor population as a function of look-back time. These effects, if they are large and not constrained or corrected, will limit our ability to accurately measure relative luminosity distances, and have the potential to reduce the efficacy of high-z type Ia SNe for measuring cosmology [74, 77, 83, 87].
K-Corrections: As SNe are observed at larger and larger redshifts, their light is shifted to longer wavelengths. Since astronomical observations are normally made in fixed band passes on Earth, corrections need to be applied to account for the differences caused by the spectrum shifting within these band passes. These corrections take the form of integrating the spectrum of an SN over the relevant band passes, shifting the SN spectrum to the correct redshift, and re-integrating. Kim et al. [43] showed that these effects can be minimized if one does not use a single bandpass, but instead chooses the bandpass closest to the redshifted rest-frame bandpass, as they had done for SN1992bi [73]. They showed that the inter-band K-correction is given by
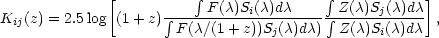 |
(10) |
where Kij(z) is the
correction to go from filter i to filter j, and
Z( ) is
the spectrum corresponding to zero magnitude of the filters.
) is
the spectrum corresponding to zero magnitude of the filters.
The brightness of an object expressed in magnitudes, as a function of z is
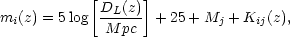 |
(11) |
where DL(z) is given by Eq. (7),
Mj is the absolute magnitude of object
in filter j, and Kij is given by Eq. (10). For
example, for H0 = 70 km s-1 Mpc-1,
and DL = 2835 Mpc
( M = 0.3,
M = 0.3,

 = 0.7), at
maximum light a SNIa has MB = - 19.5 mag
and a KBR = - 0.7 mag. We therefore expect an SNIa at
z = 0.5 to peak at mR ~ 22.1 mag for this set
of cosmological parameters.
= 0.7), at
maximum light a SNIa has MB = - 19.5 mag
and a KBR = - 0.7 mag. We therefore expect an SNIa at
z = 0.5 to peak at mR ~ 22.1 mag for this set
of cosmological parameters.
K-correction errors depend critically on three uncertainties:
The first error should not be an issue if correct observational procedures are used on an instrument that has no fundamental problems. The second error is currently estimated to be small (~ 0.01 mag), based on the consistency of spectrophotometry and broadband photometry of the fundamental standards, Sirius and Vega [5]. To improve this uncertainty will require new, careful experiments to accurately calibrate a star, such as Vega or Sirius (or a White Dwarf or solar analog star), and to carefully infer the standard bandpass that defines the photometric system in use at telescopes. The third error requires a large database to match as closely as possible an SN with the spectrophotometry used to calculate the K-corrections. Nugent et al. [58] have shown that extinction and color are related and, by correcting the spectra to force them to match the photometry of the SN needing K-corrections, that it is possible to largely eliminate errors 1 and 3, even when using spectra that are not exact matches (in epoch or in fine detail) to the SNIa being K-corrected. Scatter in the measured K-corrections from a variety of telescopes and objects allows us to estimate the combined size of the effect for the first and third errors. These appear to be ~ 0.01 mag for redshifts where the high-z and low-z filters have a large region of overlap (e.g., R-band matched to B-band at z = 0.5).
Extinction: In the nearby Universe we see SNIa in a variety of environments, and about 10% have significant extinction [30]. Since we can correct for extinction by observing two or more wavelengths, it is possible to remove any first order effects caused by a changing average extinction of SNIa as a function of z. However, second order effects, such as possible evolution of the average properties of intervening dust, could still introduce systematic errors. This problem can also be addressed by observing distant SNIa over a decade or so of wavelength in order to measure the extinction law to individual objects. Unfortunately, this is observationally very expensive. Current observations limit the total systematic effect to < 0.06 mag, as most of our current data is based on two color observations.
An additional problem is the existence of a thin veil of dust around the Milky Way. Measurements from the Cosmic Background Explorer (COBE) satellite accurately determined the relative amount of dust around the Galaxy [89], but there is an uncertainty in the absolute amount of extinction of about 2 - 3%. This uncertainty is not normally a problem, since it affects everything in the sky more or less equally. However, as we observe SNe at higher and higher redshifts, the light from the objects is shifted to the red and is less affected by the Galactic dust. Our present knowledge indicates that a systematic error as large as 0.06 mag is attributable to this uncertainty.
Selection Effects: As we discover SNe, we are subject to a variety of selection effects, both in our nearby and distant searches. The most significant effect is the Malmquist Bias - a selection effect which leads magnitude limited searches to find brighter than average objects near their distance limit since brighter objects can be seen in a larger volume than their fainter counterparts. Malmquist Bias errors are proportional to the square of the intrinsic dispersion of the distance method, and because SNIa are such accurate distance indicators these errors are quite small, ~ 0.04 mag. Monte Carlo simulations can be used to estimate such selection effects, and to remove them from our data sets [74, 76, 77, 87]. The total uncertainty from selection effects is ~ 0.01 mag and, interestingly, may be worse for lower redshift objects because they are, at present, more poorly quantified.
Gravitational Lensing: Several authors have pointed out that the radiation from any object, as it traverses the large scale structure between where it was emitted and where it is detected, will be weakly lensed as it encounters fluctuations in the gravitational potential [37, 45, 100]. On average, most of the light travel paths go through under-dense regions and objects appear de-magnified. Occasionally, the light path encounters dense regions and the object becomes magnified. The distribution of observed fluxes for sources is skewed by this process such that the vast majority of objects appear slightly fainter than the canonical luminosity distance, with the few highly magnified events making the mean of all light paths unbiased. Unfortunately, since we do not observe enough objects to capture the entire distribution, unless we know and include the skewed shape of the lensing a bias will occur. At z = 0.5, this lensing is not a significant problem: If the Universe is flat in normal matter, the large scale structure can induce a shift of the mode of the distribution by only a few percent. However, the effect scales roughly as z2, and by z = 1.5 the effect can be as large as 25% [38]. While corrections can be derived by measuring the distortion of background galaxies near the line of sight to each SN, at z > 1, this problem may be one which ultimately limits the accuracy of luminosity distance measurements, unless a large enough sample of SNe at each redshift can be used to characterize the lensing distribution and average out the effect. For the z ~ 0.5 sample, the error is < 0.02 mag, but it is much more significant at z > 1 (e.g., for SN1997ff) [4, 55], especially if the sample size is small.
Evolution: SNIa are seen to evolve in the nearby Universe. Hamuy et al. [29] plotted the shape of the SN light curves against the type of host galaxy. SNe in early hosts (galaxies without recent star formation) consistently show light curves which rise and fade more quickly than SNe in late-type hosts (galaxies with on-going star formation). However, once corrected for light curve shape the luminosity shows no bias as a function of host type. This empirical investigation provides reassurance for using SNIa as distance indicators over a variety of stellar population ages. It is possible, of course, to devise scenarios where some of the more distant SNe do not have nearby analogues, so as supernovae are studied at increasingly higher redshifts it can become important to obtain detailed spectroscopic and photometric observations of every distant SN to recognize and reject examples that have no nearby analogues.
In principle, it should be possible to use differences in the spectra and light curves between nearby and distant SNe, combined with theoretical modeling, to correct any differences in absolute magnitude. Unfortunately, theoretical investigations are not yet advanced enough to precisely quantify the effect of these differences on the absolute magnitude. A different, empirical approach to handle SN evolution [10] is to divide the SNe into subsamples of very closely matched events, based on the details of the their light curves, spectral time series, host galaxy properties, etc. A separate Hubble diagram can then be constructed for each subsample of SNe, and each will yield an independent measurement of the cosmological parameters. The agreement (or disagreement) between the results from the separate subsamples is an indicator of the total effect of evolution. A simple, first attempt at this kind of test has been performed by comparing the results for SNe found in elliptical host galaxies to SNe found in late spirals or irregular hosts, and the cosmological results from these subsamples were found to agree well [91].
Finally, it is possible to move to higher redshifts and see if the SNe deviate from the predictions of Eq. (7). At a gross level, we expect an accelerating Universe to be decelerating in the past because the matter density of the Universe increases with redshift, whereas the density of any dark energy leading to acceleration will increase at a slower rate than this (or not at all in the case of a cosmological constant). If the observed acceleration is caused by some sort of systematic effect, it is likely to continue to increase (or at least remain steady) with z, rather than disappear like the effects of dark energy. A first comparison has been made with SN1997ff at z ~ 1.7 [85], and it seems consistent with a decelerating Universe at that epoch. More objects are necessary for a definitive answer, and these should be provided by several large programs that have been discovering such type Ia SNe at the W.M. Keck Telescope I (KECK I), Subaru Telescope), and HST telescopes.