2.2. Why Do We Care?

While we would obviously like to know more clearly which population(s) of galaxies DLAs are associated with, this issue does not detract from the importance of this class of QSO absorbers for studies of element abundances, for the following reasons.

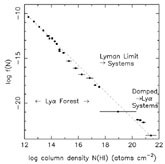Figure 5. (Reproduced from Storrie-Lombardi & Wolfe 2000). The column density distribution function of neutral hydrogen for all QSO absorbers spans ten orders of magnitude, from logN(H I) = 12 to 22 and can be adequately described by a single power law f (NH I) NH I-1.5, shown by the dashed line.

First, with neutral hydrogen column densities N(H I) 2 × 10²⁰ cm^-2, DLAs are the `heavy weights' among QSO absorption systems, at the upper end of the distribution of values of N(H I) which spans 10 orders of magnitude for all absorbers (see Figure 5). Over this entire range, f (N_H I) - defined as the number of absorbing systems per unit redshift path per unit column density - can be fitted with a single power law of the form

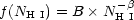(2.1)

with 1.5 (Tytler 1987; Storrie-Lombardi & Wolfe 2000). While the most numerous absorbers are those with the lowest column densities (a turn-over at low values of N(H I) has yet to be found), the high column densities of DLAs more than compensate for their relative paucity. More specifically, so long as < 2, the integral of the column density distribution

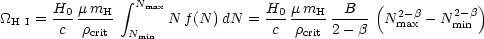(2.2)

is dominated by N_max, i.e. by DLAs (Lanzetta 1993). In eq. (2.2), H₀ is the Hubble constant, c is the speed of light, m_H is the mass of the hydrogen atom, µ is the mean atomic weight per baryon (µ = 1.4 for solar abundances; Grevesse & Sauval 1998) and _crit is the closure density

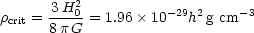(2.3)

where h is the Hubble constant in units of 100 km s^-1 Mpc^-1.

As a consequence, the mean metallicity of DLAs is the closest measure we have of the global degree of metal enrichment of neutral gas in the universe at a given epoch, irrespectively of the precise nature of the absorbers, a point often emphasised by Mike Fall and his collaborators (e.g. Fall 1996). Of course this only applies if there are no biases which exclude any particular type of high redshift object from our H I census.

Second, it is possible to determine the abundances of a wide variety of elements in DLAs with higher precision than in most other astrophysical environments in the distant universe. In particular, echelle spectra obtained with large telescopes can yield abundance measures accurate to 10-20% (e.g. Prochaska & Wolfe 2002), because: (a) the damping wings of the Ly line are very sensitive to the column density of H I; (b) several atomic transitions are often available for elements of interest; and (c) ionisation corrections are normally small, because the gas is mostly neutral and the major ionisation stages are observed directly (Vladilo et al. 2001). Dust depletions can be a complication, but even these are not as severe in DLAs as in the local interstellar medium (Pettini et al. 1997a) and can be accounted for with careful analyses (e.g. Vladilo 2002a). Thus, abundance studies in DLAs complement in a very effective way the information provided locally by stellar and nebular spectroscopy and, as we shall see, can offer fresh clues to the nucleosynthesis of elements, particularly in metal-poor environments which are difficult to probe in the nearby universe. DLAs are also playing a role in the determination of the primordial abundances of the light elements, as discussed by Gary Steigman in this volume (see also Tytler et al. 2000 and Pettini & Bowen 2001).