Coevolution of Black Holes and Galaxies, 2003
ed. L. C. Ho (Pasadena: Carnegie Observatories,
http://www.ociw.edu/ociw/symposia/series/symposium1/proceedings.html)

| Carnegie Observatories Astrophysics Series, Vol. 1:
Coevolution of Black Holes and Galaxies, 2003 ed. L. C. Ho (Pasadena: Carnegie Observatories, http://www.ociw.edu/ociw/symposia/series/symposium1/proceedings.html) |
 |
Abstract: We discuss recent work on two topics. In an in-press paper by Jaffe & Backer we calculate the spectrum of the stochastic background of gravitational radiation from the coalescence of Massive Black Holes throughout the low redshift universe. In the recent thesis work of Lommen the observational upper limit on the energy density in the stochastic background of gravitational radiation at nanoHertz frequencies is lowered by an order of magnitude. This limit places an observational bound on the very uncertain merger history of galaxies and subsequent Massive Black Hole coalescences.
The evidence for Massive Black Holes (MBHs) in the majority of spheroids at zero redshift is increasing, although the origin and mass evolution of MBHs is an outstanding mystery. The evidence for growth of galaxies by mergers is strong, although the merger rate and its evolution with redshift is uncertain. Begelman, Blandford & Rees (BBR; 1980) wrote a seminal paper on physical processes involved during the merger of galaxies containing MBHs that is followed by the coalescence of the MBHs. Rajagopal & Romani (RR; 1995) used the framework in BBR along with the classic description of gravitational radiation from a point mass binary in Peters & Matthews (1963) to estimate the stochastic background 1 spectrum of gravitational radiation (GWB). In the first section below we provide a summary of an in-press paper by Jaffe & Backer (JB; 2003) that updates the work of RR using new data on both MBH demographics and galaxy merger rate.
The driver for the calculations done in RR and in JB is the potential detection of the GWB by precision pulsar timing experiments as had been considered earlier by Sazhin (1978) and Detweiler (1979). Pulsars act as distant clocks, and their electromagnetic emissions to us are perturbed in the same manner as the laser light in gravitational wave interferometers such as LIGO or LISA. A mirror is not needed as the source is periodic. Kaspi et al. (1994) present precision timing of two millisecond pulsars over a period of seven years. This measurement is used to constrain the energy density in the GWB to less than 6 × 10-8 in units of the closure density. In the second section we summarize the Berkeley PhD effort of Lommen (2002) that extends the Kaspi et al. experiment to seventeen years and lowers the GWB energy density limit by an order of magnitude.
Prospects for future work are discussed briefly in the final section.
1.2. The Universe of Massive Black Hole
Coalescence
The goal in Jaffe & Backer is a parameterized model of the universe of MBH coalescences that can be adjusted as new data become available. There are five major ingredients which we list in order of decreasing certainty:
As stated in the introduction the emission of gravitational radiation of a point mass binary in GR is a classic result. We use the Peters & Matthews formulation to derive the wave amplitude h, a dimensionless strain, as a function of MBH masses at a given frequency at the source and redshifted into the frame of the observer. The emitted frequency is twice the orbital frequency for the assumed circular orbits, and, in turn, establishes both the luminosity and the lifetime of the binary system.
Standard cosmological parameters are used. Current uncertainties lead to small changes in the resultant GWB spectrum.
BBR present a framework for evolution of a pair of galaxies with central MBHs after the galaxies become gravitationally bound. The galaxies merge into each other on an orbital time scale owing to dynamical friction. The process continues with the central cores and their MBHs sinking toward each other. In BBR and at this conference the final fate of the MBH binary is questioned. In the simplest of spherical models dynamical friction halts when a loss cone of stars in the orbital plane develops. This may happen before the gravitational radiation time scale is sufficiently short to bring the MBHs to coalescence in a Hubble time. While there is an absence of observational evidence of stalled MBH binaries in subparsec orbits, measurements are very difficult or currently impossible and so we must say that there is no significant evidence of absence. Figure 1.1 displays the evolution time scale as a function of MBH separation following a figure in BBR. In JB we assume that nature is efficient in bringing the MBH binary from the galaxy merger separation quickly to the separation where gravitational wave decay of the orbit is rapid. That is, no Green's funtion is needed to convert between the galaxy-galaxy capture moment and the time of domination of evolution by gravitational wave emission.
We use the results in Merritt & Ferrarese (2001) to provide the MBH demographics in the local universe. In our current work, we make no adjustment to the population as a function of redshift.
The final ingredient in our model is the galaxy-galaxy merger rate. We use the recent work of Patton et al. (2002). These authors estimate the fraction of bound pairs in a large (4184) field galaxy survey. The pair separation establishes the orbit time and hence the time scale for evolution of the orbit by dynamical friction (see Fig. 1.1). We explore two models of variation of the merger rate with red shift that are within current observational limits. We have approached the model from the viewpoint of observational data at zero redshift rather than the more theoretical approach which would use a merger tree starting at high redshift.
Our results are summarized in a spectrum
(Fig. 1.2)
of the characteristic strain, hc(f ),
which is derived from the power spectral density spectrum of h by
hc2
 fPh. This allows for ease of comparison with
experimental
measurement variances at any frequency which is topic of the next section.
Both analytical and monte carlo results are presented. The most likely
redshift for source contribution is ~ 1 and some million MBH binaries
are contributing. The significant variance from a smooth septrum in the
monte carlo model indicates that a relatively small number dominate.
fPh. This allows for ease of comparison with
experimental
measurement variances at any frequency which is topic of the next section.
Both analytical and monte carlo results are presented. The most likely
redshift for source contribution is ~ 1 and some million MBH binaries
are contributing. The significant variance from a smooth septrum in the
monte carlo model indicates that a relatively small number dominate.
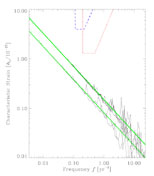 |
Figure 1.2. Characteristic strain spectrum hc(f ) for two models discussed in Jaffe & Backer (2003), along with Monte-Carlo realizations. The upper thick curve and the associated realizations have strong evolution of merger rate with z; the lower set of curves has no evolution. The dashed line gives an estimate of the current best limits on the gravitational wave background from pulsar timing observations. The dotted line shows the expected limits from a Pulsar Timing Array, after operation for ~ 8 years. |
1.3. Gravitational Wave Detection and Pulsar Timing
Experiments
Any precision measurement of length or time or energy can be used to detect
gravitational radiation. Figure 1.3 presents a
large scale view of
the stochastic GWB spectrum with limits from current and planned
experiments. The CMB anisotropy
( T / T)
places a limit on a scale-free primordial spectrum
at attoHertz frequencies. Pulsar measurements
(
T / T)
places a limit on a scale-free primordial spectrum
at attoHertz frequencies. Pulsar measurements
( t / t)
place a limit
at nanoHertz frequencies where the dominant source is likely to be from the
MBH binary population in the Universe. The LISA and LIGO instruments
will operate in the milliHertz and kiloHertz bands, respectively. LISA
will be sensitive to individual MBH-MBH coalescence events while pulsar
timing will detect only
the cacaphony of all objects with just a small level of cosmic variance from
one frequency to the next (Fig. 1.2).
t / t)
place a limit
at nanoHertz frequencies where the dominant source is likely to be from the
MBH binary population in the Universe. The LISA and LIGO instruments
will operate in the milliHertz and kiloHertz bands, respectively. LISA
will be sensitive to individual MBH-MBH coalescence events while pulsar
timing will detect only
the cacaphony of all objects with just a small level of cosmic variance from
one frequency to the next (Fig. 1.2).
 |
Figure 1.3. Characteristic strain spectrum covering all observable bands. |
Gravitational radiation perturbs the spatial part of the space-time metric from unity by an amount given by the dimensionless strain, h. For electromagnetic radiation propagation through a gravitational radiation field the strain can be treated as a perturbation of the index of refraction from unity in 3-space. Propagation of an electromagnetic wave (and therefore a pulsar pulse) from a distant source in the galaxy through integer cycles of a gravitational wave leaves no net effect. What is embedded in the pulsar arrival time is the result of propagation through fractional cycles of the gravitational wave - at the pulsar after emission and at the earth upon reception. The latter, reception effect is correlated amongst a spatial array of pulsars, and therefore we can use a Pulsar Timing Array as a Gravitational Wave Telescope.
The dimensionless strain that we are sensitive to in pulsar timing is
given by
hc ~ R / (N1/2 T /
2 ), where R is the
characteristic residual from the timing model,
N is the number of degrees of freedom, and T is the
duration of the measurement. Given that R is independent of
T in the best cases, the strain limit
improves with duration. Sensitivity to low frequency gravitational waves is
limited by duration as well as by the need to fit for a neutron star
rotation polynomial series in the timing model.
), where R is the
characteristic residual from the timing model,
N is the number of degrees of freedom, and T is the
duration of the measurement. Given that R is independent of
T in the best cases, the strain limit
improves with duration. Sensitivity to low frequency gravitational waves is
limited by duration as well as by the need to fit for a neutron star
rotation polynomial series in the timing model.
In her recent thesis work A. Lommen (2002) at Berkeley and collaborators E. Splaver and D. Nice at Princeton initiated a precision timing program the Arecibo Observatory following the upgrade completion in 1996. The best star for long term precision is the 5-millisecond pulsar B1855+09. We have tied this new experiment to the earlier Arecibo experiment presented in Kaspi et al. (1994) using lower sensitivity measurements at other telescopes. The resulting limits in Figure 1.2 follow roughly from R ~ 2 µs, N ~ 200, and T ~ 17 y. Our current limit in hc is a factor of ~ 5 above the MBH-MBH Universe model with strong evolution of the merger rate with redshift. We are in the process of defining more quantitatively the parameter space excluded by the measurements, but it seems at this time that the pulsar measurements are not highly restrictive.
The Jaffe & Backer model of MBH-MBH coalescences provides a revised estimate of the stochastic background of gravitational radiation at nanoHertz frequencies along with a new estimate of the cosmic variance in the spectrum. This model can be improved in the spectrum as new information becomes available. Furthermore the model can be improved by linking evolutionary components of the model to early Universe constraints on the growth of structure.
New precision pulsar timing measurements have lowered the bound on energy density in a stochastic background of gravitational radiation. This constrains extreme models of galaxy-galaxy merger history. Continuing measurements will employ a Pulsar Timing Array that will allow us to detect, rather than simply constrain, the spectrum.
1 Some would call this a foreground and reserve background for a primordial waves. Back.