Coevolution of Black Holes and Galaxies, 2003
ed. L. C. Ho (Pasadena: Carnegie Observatories,
http://www.ociw.edu/ociw/symposia/series/symposium1/proceedings.html)

| Carnegie Observatories Astrophysics Series, Vol. 1:
Coevolution of Black Holes and Galaxies, 2003 ed. L. C. Ho (Pasadena: Carnegie Observatories, http://www.ociw.edu/ociw/symposia/series/symposium1/proceedings.html) |
 |
Abstract: Recent years have seen tremendous progress in the quest to detect supermassive black holes in the centers of nearby galaxies, and gas-dynamical measurements of the central masses of active galaxies have been valuable contributions to the local black hole census. This review summarizes measurement techniques and results from observations of spatially resolved gas disks in active galaxies, and reverberation mapping of the broad-line regions of Seyfert galaxies and quasars. Future prospects for the study of black hole masses in active galaxies, both locally and at high redshift, are discussed.
The detection of supermassive black holes in the nuclei of many nearby galaxies has been one of the most exciting discoveries in extragalactic astronomy during the past decade. Accretion onto black holes has long been understood as the best explanation for the enormous luminosities of quasars (Zel'dovich & Novikov 1964; Salpeter 1964; Rees 1984), and the luminosity generated by quasars over the history of the universe implies that most large galaxies must contain a black hole as a relic of an earlier quasar phase (Soltan 1982; Chokshi & Turner 1992; Small & Blandford 1992). While the search for evidence of black holes in nearby galaxies began 25 years ago with the seminal studies of M87 by Sargent et al. (1978) and Young et al. (1978), only a handful of galaxies were accessible to such measurements until the repair of the Hubble Space Telescope (HST) in 1993 made it possible to study the central dynamics of galaxies routinely at 0."1 resolution. Also within the past decade, the advent of 8 and 10-meter class ground-based telescopes has opened a new vista on our own Galactic center (see Ghez, this volume), and very long baseline interferometry observations revealed stunning dynamical evidence for a black hole in the Seyfert 2 galaxy NGC 4258 (Miyoshi et al. 1995). These developments and many others have led not only to the recognition that supermassive black holes actually do exist, but to the realization that the growth of black holes must be an integral component of the galaxy formation process.
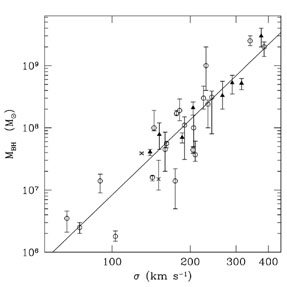 |
Figure 1.1. The correlation between black hole mass and stellar velocity dispersion. Triangles denote galaxies measured with HST observations of gas dynamics, crosses are H2O maser galaxies, and circles denote stellar-dynamical detections. The diagonal line is the best fit to the data as determined by Tremaine et al. (2002). |
With measurements of black hole masses in several galaxies, it became
possible for the first time to study the demographics of the black
hole population and the connection of the black holes with their host
galaxies.
Kormendy & Richstone (1995)
showed that MBH was correlated with
Lbulge, the luminosity of the spheroidal "bulge"
component of the host galaxy, albeit with substantial scatter. More
intriguing was the discovery that MBH is very tightly
correlated with
 *,
the stellar velocity dispersion in the host galaxy
(Ferrarese & Merritt 2000;
Gebhardt et al. 2000a).
The scatter in this relation is surprisingly small;
Tremaine et al. (2002)
estimate the dispersion to be < 0.3 dex in log
MBH at a given value of
*,
the stellar velocity dispersion in the host galaxy
(Ferrarese & Merritt 2000;
Gebhardt et al. 2000a).
The scatter in this relation is surprisingly small;
Tremaine et al. (2002)
estimate the dispersion to be < 0.3 dex in log
MBH at a given value of
 *.
This is a remarkable finding: it implies that the masses
of black holes, objects that inhabit scales of
*.
This is a remarkable finding: it implies that the masses
of black holes, objects that inhabit scales of
 10-4 pc in
galaxy nuclei, are almost completely determined by the bulk
properties of their host galaxies on scales of hundreds or thousands
of parsecs. Although the MBH -
10-4 pc in
galaxy nuclei, are almost completely determined by the bulk
properties of their host galaxies on scales of hundreds or thousands
of parsecs. Although the MBH -
 *
correlation is well established,
its slope, and the amount of intrinsic scatter, remain somewhat
controversial. The currently available sample of galaxies with
accurate determinations of
MBH is still modest. More measurements
of black hole masses in nearby galaxies, over the widest possible
range of host galaxy types and velocity dispersions, are needed in
order to obtain a definitive present-day black hole census.
*
correlation is well established,
its slope, and the amount of intrinsic scatter, remain somewhat
controversial. The currently available sample of galaxies with
accurate determinations of
MBH is still modest. More measurements
of black hole masses in nearby galaxies, over the widest possible
range of host galaxy types and velocity dispersions, are needed in
order to obtain a definitive present-day black hole census.
Gas-dynamical measurements of black hole masses in active galactic nuclei (AGNs) are an essential contribution to this pursuit, as illustrated in Figure 1.1. HST observations of ionized gas disks are vitally important for tracing the upper end of the black hole mass function, where stellar-dynamical measurements are hampered both by the low stellar surface brightness of the most massive elliptical galaxies and by the possibility of velocity anisotropy in nonrotating ellipticals. Maser observations have provided the most solid black hole detection outside of our own Galaxy, strengthening the case that the massive dark objects discovered in HST surveys are indeed likely to be supermassive black holes. Reverberation mapping, and secondary methods that are calibrated by comparison with the reverberation technique, offer the most promising methods to determine black hole masses at high redshift.
The topic of black holes in active galaxies is vast, and this review will only concentrate on gas-dynamical measurements of black hole masses in AGNs. Before discussing the methods and results, a few general comments are in order. As Kormendy & Richstone (1995) have pointed out, there is a potentially serious drawback to any measurement technique based on gas dynamics: unlike stars, gas can respond to nongravitational forces, and the motions of gas clouds do not always reflect the underlying gravitational potential. For all methods based on gas dynamics, it is absolutely crucial to verify that the gas is actually in gravitational orbits about the central mass. If, for example, AGN-driven outflows or other non-gravitational motions dominate, then black hole masses derived under the assumption of gravitational dynamics will be seriously compromised or completely erroneous. With that said, there are now numerous examples of ionized gas disks, and at least one maser disk, that clearly show orderly circular rotation. For reverberation mapping, the dynamical state of the broad-line emitting gas is more difficult to ascertain, but as discussed in Section 1.4 below, recent observations have provided some encouragement.
It must also be emphasized that, while these measurement techniques are capable of detecting dark mass concentrations in the centers of galaxies and determining their masses with varying degrees of accuracy, the observations do not actually prove that the dark mass is in the form of a supermassive black hole. The spatial resolution of gas-dynamical observations with HST typically corresponds to ~ 105-6 Schwarzschild radii; this is often sufficient to resolve the region over which the black hole dominates the gravitational potential of its host galaxy, but it is far from the resolution needed in order to detect relativistic motion in the strong gravitational field near the black hole's event horizon. The conclusion that the massive dark objects detected in nearby galaxies are actually black holes is supported by the two most convincing dynamical detections, in our own Galaxy and in NGC 4258; in both objects the density of the central dark mass is inferred to be so large that reasonable alternatives to a black hole can be ruled out (Maoz 1998). The best evidence for highly relativistic motion in the inner accretion disks of AGNs comes from X-ray spectra showing extremely broadened (~ 0.3c), gravitationally redshifted Fe K line emission in Seyfert nuclei (Tanaka et al. 1995; Nandra et al. 1997). While this signature has only been convincingly detected in a handful of objects, it offers a powerful confirmation of the AGN paradigm, and analysis of the relativistically broadened line profiles may even reveal evidence for the black hole's spin (e.g., Iwasawa et al. 1996).
1.2. Black Hole Masses from Dynamics of Ionized Gas
Disks
A striking discovery from the first years of HST observations was the presence of round, flattened disks of ionized gas and dust in the centers of some nearby radio galaxies (Jaffe et al. 1993; Ford et al. 1994). It was previously known from ground-based imaging that many ellipticals contained nuclear patches of dust (Kotanyi & Ekers 1979; Sadler & Gerhard 1985), but HST revealed that the dust was often arranged in well-defined disks too small to be resolved from the ground. Imaging surveys with HST have found such disks, with typical radii of 100 - 1000 pc, in ~ 20% of giant elliptical galaxies (e.g., Verdoes Kleijn et al. 1999; de Koff et al. 2000; Tran et al. 2001).
Jaffe et al. (1999) show that nuclear gas disks in early-type galaxies fall into two general categories. The most common type are dusty disks, which are easily detected by their obscuration in broad-band optical HST images. In radio galaxies with flattened dust disks, the radio axis is usually nearly perpendicular to the disk plane (de Koff et al. 2000). The dust is usually accompanied by an ionized component. Figure 1.2 shows an example, the disk in the S0 galaxy NGC 3245. The second class consists of ionized gas disks without associated dust. M87 (Ford et al. 1994) is the prototype of this category. Ionized disks are sometimes found to have filamentary or spiral structure.
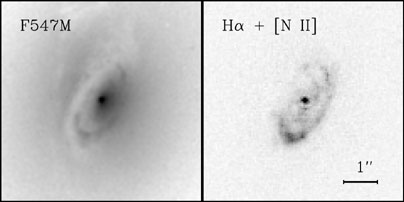 |
Figure 1.2. An example of a dusty
emission-line disk: HST images of the
S0 galaxy NGC 3245. The left panel is a continuum image taken with
the HST F547M filter (equivalent to the V band), and the
right panel shows a continuum-subtracted, narrow-band image isolating the
H |
Soon after the first HST servicing mission, the first spectroscopic
investigations of the kinematics of these disks were performed with
the Faint Object Spectrograph (FOS). The first target was M87, for
which Harms et al. (1994)
detected a steep velocity gradient across
the nucleus in the H ,
[N II], and [O III] emission
lines, consistent with Keplerian rotation in an inclined disk. The
central mass was found to be (2.4 × 0.7) × 109
M
,
[N II], and [O III] emission
lines, consistent with Keplerian rotation in an inclined disk. The
central mass was found to be (2.4 × 0.7) × 109
M ,
remarkably close to the values first determined by
Young et al. (1978)
and Sargent et al. (1978).
The second gas-dynamical study with HST found a central dark mass
of (4.9 × 1.0) × 108
M
,
remarkably close to the values first determined by
Young et al. (1978)
and Sargent et al. (1978).
The second gas-dynamical study with HST found a central dark mass
of (4.9 × 1.0) × 108
M in the
radio galaxy NGC 4261
(Ferrarese, Ford, & Jaffe 1996).
These dramatic results opened a new chapter in the search for supermassive
black holes, demonstrating that spatially resolved gas disks could
indeed be used to measure the central masses of galaxies. In contrast
to stellar dynamics, the gas-dynamical method is extremely appealing
in its simplicity. Modeling the kinematics of a thin, rotating disk
is conceptually straightforward. Furthermore, observations of
emission-line velocity fields require less telescope time than
absorption-line spectroscopy.
in the
radio galaxy NGC 4261
(Ferrarese, Ford, & Jaffe 1996).
These dramatic results opened a new chapter in the search for supermassive
black holes, demonstrating that spatially resolved gas disks could
indeed be used to measure the central masses of galaxies. In contrast
to stellar dynamics, the gas-dynamical method is extremely appealing
in its simplicity. Modeling the kinematics of a thin, rotating disk
is conceptually straightforward. Furthermore, observations of
emission-line velocity fields require less telescope time than
absorption-line spectroscopy.
After these initial detections, progress was made on two fronts. The installation of the Space Telescope Imaging Spectrograph (STIS), a long-slit instrument, greatly expanded the capabilities of HST for dynamical measurements, making it possible to perform surveys of large numbers of galaxies. In addition, the development of techniques to model the kinematic data in detail led to more robust measurements. At the center of a disk, the large spatial gradients in rotation velocity and emission-line surface brightness are smeared out by the telescope point-spread function (PSF) and by the nonzero size of the spectroscopic aperture. Macchetto et al. (1997) were the first to model the effects of instrumental blurring on HST gas-kinematic data, in their analysis of long-slit spectra of the M87 disk, and detailed descriptions of modeling techniques have been given by Barth et al. (2001), Maciejewski & Binney (2001), and Marconi et al. (2003).
The feasibility of performing a black hole detection in any given
galaxy can be roughly quantified in terms of
rG, the radius of the
"sphere of influence" over which the black hole dominates the
gravitational potential of its host galaxy. This quantity is given by
rG = G M
Detection of black holes via their influence on the motions of stars
or gas is most readily accomplished when observations are able to
probe spatial scales smaller than
rG, but it should be borne in mind
that this is at best an approximate criterion. The stellar velocity
dispersion is an aperture-dependent quantity, so there is no uniquely
determined value of rG for a given galaxy. Even when
rG is
unresolved the black hole will still influence the motions of stars
and gas at larger radii. In stellar-dynamical measurements, it is
possible to obtain information from spatial scales smaller than the
instrumental resolution by measuring higher-order moments of the
central line-of-sight velocity profile, since extended wings on the
velocity profile are the signature of high-velocity stars orbiting
close to the black hole (e.g.,
van der Marel 1994).
This technique
cannot generally be applied to gas-dynamical measurements, however,
because it would require knowledge of the emissivity profile of the
gas on spatial scales smaller than the instrumental resolution.
The analysis of a gas-dynamical dataset consists of the following
basic steps. The galaxy's stellar light profile must be measured,
corrected for dust absorption if necessary, and converted to a
three-dimensional luminosity density. A model velocity field is
computed for the combined potential of the black hole and the galaxy
mass distribution, usually assuming a spatially constant stellar
mass-to-light ratio. After projecting the velocity field to a given
distance and inclination angle, the model is synthetically
"observed" by simulating the passage of light through the
spectrograph optics and measuring the resulting model line profiles.
Finally, the model fit to the measured emission-line velocity field is
optimized to obtain the best-fitting value of
MBH. In addition to MBH, the free
parameters in the kinematic model fit include the disk
inclination and major axis position angle, and the stellar
mass-to-light ratio; these can be determined from the kinematic data
if observations are obtained at three or more parallel positions of
the spectrograph slit. With up-to-date analysis techniques and
high-quality STIS data, it is possible to achieve formal measurement
uncertainties on MBH of order ~ 25% or better for
galaxies with well-behaved disks (e.g.,
Barth et al. 2001).
This makes the gas-dynamical method very competitive with the precision
that can be achieved by stellar-dynamical measurements.
Figure 1.3 illustrates model calculations for the
projected radial velocities along the major axis of an inclined gas
disk. The models have been calculated for a disk inclined at
60° to the line of sight, in a galaxy at a distance of 20 Mpc
with MBH = 0, 107, 108, and
109
M
The middle ground between these two extremes is illustrated by the
108
M
Since the gas can respond to non-gravitational forces, it is essential
for the observations to map the disk structure in sufficient detail
that the assumption of gravitational motion can be tested. This is a
nontrivial concern, as there are examples of galaxies in which the gas
does not rotate at the circular velocity (e.g.,
Fillmore, Boroson, & Dressler 1986;
Kormendy & Westpfahl 1989).
The case of IC 1459 serves
as a cautionary tale. FOS observations at 6 positions within 0."3
of the nucleus revealed a steep central velocity gradient in the
ionized gas, and disk model fits implied the presence of a central
dark mass of (1 - 4) × 108
M
Most of the nuclear disks observed spectroscopically with HST have
revealed evidence for substantial internal velocity dispersions, even
when the velocity field is clearly dominated by rotation. That is,
the gas disks are not in purely quiescent circular rotation, and the
disks have some degree of internal velocity structure or turbulence.
The intrinsic emission-line velocity dispersion
The origin of this internal velocity dispersion is unknown, and the
interpretation of
Since different groups have used a variety of methods to treat this
problem in dynamical analyses (sometimes ignoring it altogether), and
since
Most gas-dynamical studies to date have concentrated on elliptical and
S0 galaxies, but STIS data have now been obtained for dozens of spiral
galaxies as well (e.g.,
Marconi et al. 2003).
In principle, the
gas-dynamical method can work equally well for spirals, but there are
some additional complications. One is the presence of nuclear star
clusters, which are nearly ubiquitous in late-type spirals
(Carollo, Stiavelli, & Mack 1998;
Böker et al. 2002).
The nuclear star clusters are typically young
(Walcher et al. 2003),
and the dynamical
modeling must take into account the possible radial gradient in M
/ L.
Another caveat is that spiral arms or bar structure can lead to
departures from circular rotation in the ionized gas
(Koda & Wada 2002;
Maciejewski 2003).
Only ~ 10 - 20% of spirals appear to have
orderly emission-line velocity fields suitable for disk-model fitting
to derive MBH
(Sarzi et al. 2001),
so some care is needed when
selecting targets for HST gas-dynamical surveys.
Ho et al. (2002)
have shown that orderly rotation in the emission-line gas almost
exclusively occurs in galaxies having orderly, symmetric circumnuclear
dust-lane morphology that can be detected in HST imaging data, and
this offers a promising way to maximize the rate of successful
MBH measurements in future programs.
Even when gas-dynamical data cannot provide a direct measurement of
black hole mass, either due to insufficient resolution or irregular
kinematics, they can still be used to derive upper limits to
MBH from the central amplitude of the rotation curve
or the central emission-line width. For galaxies with
Gas-dynamical measurements using HST data have now been published
for about a dozen galaxies
(Harms et al. 1994;
Ferrarese et al. 1996;
Macchetto et al. 1997;
van der Marel & van den Bosch 1998;
Bower et al. 1998;
Ferrarese & Ford 1999;
Sarzi et al. 2001;
Barth et al. 2001;
Verdoes Kleijn et al. 2002;
Marconi et al. 2003).
The results,
together with stellar-dynamical measurements, have been compiled by
Kormendy & Gebhardt (2001),
Merritt & Ferrarese (2001), and
Tremaine et al. (2002).
This number will continue to increase over the next
several years, since STIS gas-kinematic observations have been
obtained or scheduled for over 100 galaxies. However, it remains to
be seen how many of these datasets will lead to accurate measurements
of black hole masses. A substantial fraction of the galaxies will
probably not have well-behaved gas disks suitable for modeling, and in
many of the target galaxies rG may be much smaller
than the resolution limit of HST
(Merritt & Ferrarese 2001).
Thus, it remains worthwhile to search for additional nearby galaxies having
morphologically regular disks that will make promising targets for
future spectroscopic observations.
With the small projected sizes of
rG in most nearby galaxies,
ground-based observations cannot generally be used to perform
gas-dynamical measurements of
MBH. One exception is the nearby (D = 3.5 Mpc)
radio galaxy Cen A.
Marconi et al. (2001)
obtained near-infrared spectra of this galaxy in 0."5 seeing, and
measured the velocity field of the
Pa
Water vapor maser emission at
A detailed review of the properties of the NGC 4258 maser system and a
listing of other known H2O maser galaxies is given by
Moran, Greenhill, & Herrnstein (1999).
Hundreds of galaxies have been surveyed for H2O masers (e.g.,
Braatz, Wilson, & Henkel 1996;
Greenhill et al. 2002,
2003),
and there are about 30 known sources to date.
Braatz et al. (1997)
find that powerful H2O masers are only
detected in Seyfert 2 and LINER nuclei, and not in Seyfert 1 galaxies.
This is consistent with the geometrical picture of AGN unification
models, which posit the existence of an edge-on torus or disk in the
type 2 objects. The large path length along our line of sight in an
edge-on disk permits maser amplification, while a more face-on disk in
a Type 1 AGN would not emit maser lines in our direction. Further
confirmation of this geometric structure comes from detection of large
X-ray obscuring columns (e.g.,
Makishima et al. 1994;
Iwasawa, Maloney, & Fabian 2002)
and polarized emission lines from obscured nuclei (e.g.,
Antonucci & Miller 1985;
Wilkes et al. 1995)
in some H2O maser galaxies.
Disklike structures have been detected in several other maser
galaxies, but NGC 4258 remains the only one for which the central mass
has been derived with high precision. The maser clouds in NGC 1068
appear to trace the surface of a geometrically thick torus rather than
a thin disk and their velocities fall below a Keplerian curve,
suggesting a central mass of ~ 107
M
Reverberation mapping uses temporal variability of active nuclei to
probe the size and structure of the broad-line region (BLR) of Seyfert
1 nuclei and quasars. The basic principle is that variability in the
ionizing photon output of the central engine will be followed by
corresponding variations in the emission-line luminosity, after a time
delay dependent on the light-travel time between the ionizing source
and the emission-line clouds
(Blandford & McKee 1982).
By monitoring
the continuum and emission-line brightness of a broad-lined AGN over a
sufficient time period, the lag between continuum variations and
emission-line response can be derived, giving a size scale for the
region emitting the line; typical sizes range from a few light-days up
to ~ 1 light-year. Thus, the method makes use of the time domain
to resolve structures that cannot be resolved spatially, and the
measurement accuracy depends on temporal sampling rather than spatial
resolution. The literature on reverberation mapping is extensive, and
this brief summary will concentrate on just a few recent results. A
thorough review of the observational and analysis techniques used in
reverberation-mapping campaigns is given by
Peterson (2001).
If the motions in the BLR are dominated by gravity (rather than, for
example, radiatively-driven outflows), then the central mass can be
derived from the BLR radius combined with a characteristic velocity.
Essentially, the black hole mass is derived as
MBH = f v2 r / G, where
v is some measure of the broad-line velocity width (typically the
full width at half maximum), r is the BLR radius derived from the
measured time delay, and f is an order-unity factor that depends on
the geometry of the BLR (i.e., disklike or spherical). Reverberation
masses for 34 Seyfert 1 galaxies and low-redshift quasars have been
determined by
Wandel, Peterson & Malkan (1999)
and Kaspi et al. (2000).
The method is subject to some potentially serious systematic
errors, however, as emphasized by
Krolik (2001);
the unknown geometry
and emissivity distribution of the BLR clouds can lead to biases in
the derived masses, and it is critically important to verify that the
BLR velocity field is in fact dominated by gravitational motion.
Recent observations have yielded some encouraging results. Since the
BLR is radially stratified in ionization level, highly ionized clouds
emitting He IIand C IV respond most quickly to continuum
variations, with response times of a few days, while lines such as
H
Another key question is whether reverberation mapping yields black
hole masses that are consistent with the host galaxy properties of the
AGNs. Gebhardt et al. (2000b)
and Ferrarese et al. (2001)
demonstrated that the reverberation masses and velocity dispersions of
several Seyfert nuclei are in good agreement with the
MBH -
Overall, the agreement between the
MBH -
Reverberation mapping can be extended to higher redshifts, since it is
not dependent on spatial resolution, but the longer variability
timescales for higher-mass black holes in luminous quasars, combined
with cosmological time dilation, can require monitoring campaigns with
durations that are a significant fraction of an individual
astronomer's career!
Kaspi et al. (2003)
present preliminary results
from an ongoing, eight-year campaign to monitor 11 luminous quasars at
2.1 < z < 3.2. Continuum variations have been detected, but the
corresponding emission-line variability has not yet been seen.
Reverberation observations of quasars are a fundamental
probe of black hole masses at high redshift, and efforts to monitor
additional quasars over a wide redshift range should be encouraged,
despite the long timescales involved.
One important result of the reverberation campaigns has been the
detection of an empirical correlation between the BLR radius and the
optical continuum luminosity, usually measured at 5100 Å
(Wandel, Malkan, & Peterson 1999;
Kaspi et al. 2000).
With a sample of 34 reverberation-mapped AGNs,
Kaspi et al. (2000)
find rBLR
These secondary methods are extremely valuable since they offer the
most straightforward estimates of black hole masses at high redshift,
although there are potential biases that must be kept in mind. The
derived BLR size and
MBH depend on the observed continuum
luminosity, but this can be affected by dust extinction
(Baker & Hunstead 1995),
or by relativistic beaming of synchrotron emission in radio-loud objects
(Whiting, Webster, & Francis 2001).
If the BLR
has a flattened, disklike geometry, then the effects of source
orientation on the observed linewidth must be accounted for (e.g.,
McLure & Dunlop 2002).
An additional concern is that the rBLR-L
relation has only been calibrated against the Kaspi et al. reverberation
sample, which covers a somewhat limited range both in
black hole mass (MBH
I conclude with a very incomplete list of a few important and
tractable problems that can be addressed in the foreseeable future by
new observations.
1. More dynamical measurements of black hole masses in nearby galaxies
are needed, over the widest possible range of host galaxy masses
and velocity dispersions, so that the slope of the
MBH -
2. Direct comparisons of stellar and gas-dynamical measurements for
the same galaxies are a needed consistency check that should be
performed for galaxies over a wide range in
3. What causes the intrinsic velocity dispersion observed in nuclear
gas disks? Is it possible to determine central masses
accurately for disks having
4. What can we learn about black hole demographics from AGNs at the
extremes of the Hubble sequence? The broad-line widths and
continuum luminosities of high-redshift quasars imply masses of up
to ~ 1010
M
5. How do the
MBH -
 *2.
Projected onto the sky, and scaled to
typical parameters for an HST measurement, this corresponds to
*2.
Projected onto the sky, and scaled to
typical parameters for an HST measurement, this corresponds to
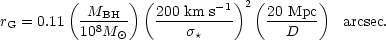
(1)
 .
To demonstrate the effects of varying
MBH, the same stellar mass profile has been used
for all four models. The model velocity fields have been convolved
with the STIS PSF and sampled over an aperture corresponding to an
0."1-wide slit, and the curves represent the mean velocity that
would be observed as a function of position along the slit. At one
extreme, the sphere of influence of the 107
M
.
To demonstrate the effects of varying
MBH, the same stellar mass profile has been used
for all four models. The model velocity fields have been convolved
with the STIS PSF and sampled over an aperture corresponding to an
0."1-wide slit, and the curves represent the mean velocity that
would be observed as a function of position along the slit. At one
extreme, the sphere of influence of the 107
M black hole is unresolved, and the 107
M
black hole is unresolved, and the 107
M model is barely distinguishable from
the model with no black hole. The unresolved Keplerian emission can
still be observed in the form of high-velocity wings on the central
line profile, but this is of little use in determining
MBH. The opposite extreme is the 109
M
model is barely distinguishable from
the model with no black hole. The unresolved Keplerian emission can
still be observed in the form of high-velocity wings on the central
line profile, but this is of little use in determining
MBH. The opposite extreme is the 109
M black hole, for which the
Keplerian region is extremely well resolved and the black hole would
be readily detected. Instrumental blurring causes a turnover in the
velocity curves at about 0."15 in this case, and Keplerian
rotation can only be clearly detected at larger radii. Thus,
Keplerian rotation can only be verified in detail (in the sense of
having several independent data points to trace the
v
black hole, for which the
Keplerian region is extremely well resolved and the black hole would
be readily detected. Instrumental blurring causes a turnover in the
velocity curves at about 0."15 in this case, and Keplerian
rotation can only be clearly detected at larger radii. Thus,
Keplerian rotation can only be verified in detail (in the sense of
having several independent data points to trace the
v  r-1/2 dependence) for galaxies with exceptionally
well-resolved rG. To date, the only published
HST gas-dynamical measurements
that have unambiguously detected the Keplerian region are those of M87
(Macchetto et al. 1997)
and M84
(Bower et al. 1998).
r-1/2 dependence) for galaxies with exceptionally
well-resolved rG. To date, the only published
HST gas-dynamical measurements
that have unambiguously detected the Keplerian region are those of M87
(Macchetto et al. 1997)
and M84
(Bower et al. 1998).
 black hole in Figure 1.3. In this case, the
Keplerian rise in velocity is not detected; instead, a steep but
smooth velocity gradient across the nucleus is observed. The mass of
the black hole can still be determined from the steepness of this
central gradient, provided that the observations give sufficient
information to distinguish the velocity curves from those of the
MBH = 0
case. It is possible in principle to measure MBH even in
galaxies for which
rG is formally unresolved, if it can be shown
that the disk has an excess rotation velocity relative to the
best-fitting model without a black hole. However, in such cases there
are practical complications that may limit the measurement accuracy:
it is critical to determine the stellar luminosity density profile and
mass-to-light ratio accurately, and spatial gradients in M /
L are an
added complication. In general, the most confident detections of
black holes will be in those relatively rare objects for which the
Keplerian region can be clearly traced, but the majority of
gas-dynamical mass measurements will come from objects for which the
mass is determined primarily from the steepness of the central
velocity gradient rather than from fitting models to a well-resolved
Keplerian velocity field.
black hole in Figure 1.3. In this case, the
Keplerian rise in velocity is not detected; instead, a steep but
smooth velocity gradient across the nucleus is observed. The mass of
the black hole can still be determined from the steepness of this
central gradient, provided that the observations give sufficient
information to distinguish the velocity curves from those of the
MBH = 0
case. It is possible in principle to measure MBH even in
galaxies for which
rG is formally unresolved, if it can be shown
that the disk has an excess rotation velocity relative to the
best-fitting model without a black hole. However, in such cases there
are practical complications that may limit the measurement accuracy:
it is critical to determine the stellar luminosity density profile and
mass-to-light ratio accurately, and spatial gradients in M /
L are an
added complication. In general, the most confident detections of
black holes will be in those relatively rare objects for which the
Keplerian region can be clearly traced, but the majority of
gas-dynamical mass measurements will come from objects for which the
mass is determined primarily from the steepness of the central
velocity gradient rather than from fitting models to a well-resolved
Keplerian velocity field.
 (Verdoes Kleijn et al. 2000).
More recently, STIS observations have mapped out the circumnuclear
kinematics in much greater detail and found an irregular and
asymmetric velocity field that cannot be interpreted in terms of flat
disk models; a stellar-dynamical analysis finds
MBH = (2.6 ± 1) × 109
M
(Verdoes Kleijn et al. 2000).
More recently, STIS observations have mapped out the circumnuclear
kinematics in much greater detail and found an irregular and
asymmetric velocity field that cannot be interpreted in terms of flat
disk models; a stellar-dynamical analysis finds
MBH = (2.6 ± 1) × 109
M (Cappellari et al. 2002).
Thus, the ionized gas fails to be a useful probe of the gravitational
potential in this galaxy.
(Cappellari et al. 2002).
Thus, the ionized gas fails to be a useful probe of the gravitational
potential in this galaxy.
 gas tends
to be greatest at the nucleus, and observed values span a wide range,
exceeding 500 km s-1 in extreme cases (e.g.,
van der Marel & van den Bosch 1998).
gas tends
to be greatest at the nucleus, and observed values span a wide range,
exceeding 500 km s-1 in extreme cases (e.g.,
van der Marel & van den Bosch 1998).
 gas
remains the single most important unresolved
problem for gas-dynamical measurements of black hole masses. In a
study of the radio galaxy NGC 7052,
van der Marel & van den Bosch (1998)
argued that
gas
remains the single most important unresolved
problem for gas-dynamical measurements of black hole masses. In a
study of the radio galaxy NGC 7052,
van der Marel & van den Bosch (1998)
argued that
 gas was
due to local turbulence in gas that
remained in bulk motion on circular orbits at the local circular
velocity. Another possibility that has been considered is that the
disks are composed of a large number of clouds with small filling
factor, and that the individual clouds are on noncircular orbits that
are nevertheless dominated by gravity (e.g.,
Verdoes Kleijn et al. 2000).
This is analogous to the effect of "asymmetric drift" that
is well-known in stellar dynamics (e.g.,
Binney & Tremaine 1987).
In this situation, the gas disk would be supported against gravity by
both rotation and random motions, and models based on pure circular
rotation would underestimate the true black hole masses. The
asymmetric drift correction to MBH is expected to be
small when
(
gas was
due to local turbulence in gas that
remained in bulk motion on circular orbits at the local circular
velocity. Another possibility that has been considered is that the
disks are composed of a large number of clouds with small filling
factor, and that the individual clouds are on noncircular orbits that
are nevertheless dominated by gravity (e.g.,
Verdoes Kleijn et al. 2000).
This is analogous to the effect of "asymmetric drift" that
is well-known in stellar dynamics (e.g.,
Binney & Tremaine 1987).
In this situation, the gas disk would be supported against gravity by
both rotation and random motions, and models based on pure circular
rotation would underestimate the true black hole masses. The
asymmetric drift correction to MBH is expected to be
small when
( gas /
vrot)2 << 1, but this must be tested on a
case by case basis by computing models for the emission-line widths.
Various approaches to calculating the asymmetric drift in gas disks
have been presented by
Cretton, Rix, & de Zeeuw (2000),
Verdoes Kleijn et al. (2000,
2002),
and Barth et al. (2001).
gas /
vrot)2 << 1, but this must be tested on a
case by case basis by computing models for the emission-line widths.
Various approaches to calculating the asymmetric drift in gas disks
have been presented by
Cretton, Rix, & de Zeeuw (2000),
Verdoes Kleijn et al. (2000,
2002),
and Barth et al. (2001).
 gas varies
widely among different galaxies, the influence of
the intrinsic velocity dispersion could be responsible for some of the
apparent scatter in the MBH -
gas varies
widely among different galaxies, the influence of
the intrinsic velocity dispersion could be responsible for some of the
apparent scatter in the MBH -
 *
relation. Now that large samples of
galaxies have been observed with STIS, it may be possible to discern
whether there are any correlations of
*
relation. Now that large samples of
galaxies have been observed with STIS, it may be possible to discern
whether there are any correlations of
 gas with
the level of nuclear
activity or with the Hubble type or any other property of the host
galaxy; detection of any clear trends might help to elucidate the
origin of the intrinsic dispersion. Three-dimensional
hydrodynamical simulations have evolved to the point where it is now
becoming feasible to model the turbulent structure of gas disks in
galaxies (e.g.,
Wada, Meurer, & Norman 2002);
this work may lead to new insights on how best to interpret
gas with
the level of nuclear
activity or with the Hubble type or any other property of the host
galaxy; detection of any clear trends might help to elucidate the
origin of the intrinsic dispersion. Three-dimensional
hydrodynamical simulations have evolved to the point where it is now
becoming feasible to model the turbulent structure of gas disks in
galaxies (e.g.,
Wada, Meurer, & Norman 2002);
this work may lead to new insights on how best to interpret
 gas in
gas-dynamical
measurements. Further discussion of the intrinsic velocity dispersion
problem is presented by
Verdoes Kleijn et al. (2003).
gas in
gas-dynamical
measurements. Further discussion of the intrinsic velocity dispersion
problem is presented by
Verdoes Kleijn et al. (2003).
 *
*
 100
km s-1, where direct measurements of
MBH are scarce, upper limits are
valuable additions to the black hole census. For example, from a
large sample of ground-based rotation curves,
Salucci et al. (2000)
demonstrated that late-type spirals must generally have
MBH
100
km s-1, where direct measurements of
MBH are scarce, upper limits are
valuable additions to the black hole census. For example, from a
large sample of ground-based rotation curves,
Salucci et al. (2000)
demonstrated that late-type spirals must generally have
MBH
 106-7
M
106-7
M .
Sarzi et al. (2002)
measured upper limits to MBH from the central
emission-line widths observed in STIS spectra of 16 galaxies having
.
Sarzi et al. (2002)
measured upper limits to MBH from the central
emission-line widths observed in STIS spectra of 16 galaxies having
 *
between 80 and 270 km s-1. The derived
upper limits are consistent with the
MBH -
*
between 80 and 270 km s-1. The derived
upper limits are consistent with the
MBH -
 *
relation, further
confirming that few galaxies (perhaps none) are strong outliers with
very overmassive black holes relative to their bulge luminosity or
velocity dispersion.
*
relation, further
confirming that few galaxies (perhaps none) are strong outliers with
very overmassive black holes relative to their bulge luminosity or
velocity dispersion.
 and
[Fe II] emission lines.
They detected a steep central velocity gradient with a turnover to
Keplerian rotation outside the region dominated by atmospheric seeing,
and derived a central dark mass of
2+3.0-1.4 × 108
M
and
[Fe II] emission lines.
They detected a steep central velocity gradient with a turnover to
Keplerian rotation outside the region dominated by atmospheric seeing,
and derived a central dark mass of
2+3.0-1.4 × 108
M .
Although the black hole mass was not determined with very high
precision, this measurement serves as a proof of concept
that ground-based observations of near-infrared emission lines can be
used for gas-dynamical analysis. In the future, near-infrared
integral-field spectrographs, coupled with laser-guided adaptive
optics on 8-10m or larger telescopes, will make it possible to pursue
such measurements from the ground routinely, at spatial resolution
comparable to that of HST in the optical. Also, the Atacama
Large Millimeter Array will provide new high-resolution
views of circumnuclear disks and new probes of disk dynamics with
molecular emission lines.
.
Although the black hole mass was not determined with very high
precision, this measurement serves as a proof of concept
that ground-based observations of near-infrared emission lines can be
used for gas-dynamical analysis. In the future, near-infrared
integral-field spectrographs, coupled with laser-guided adaptive
optics on 8-10m or larger telescopes, will make it possible to pursue
such measurements from the ground routinely, at spatial resolution
comparable to that of HST in the optical. Also, the Atacama
Large Millimeter Array will provide new high-resolution
views of circumnuclear disks and new probes of disk dynamics with
molecular emission lines.
1.3. Black Hole Masses from Observations of
H2O Masers
 = 1.35 cm from the
nucleus of the low-luminosity Seyfert 2 galaxy NGC 4258 was detected by
Claussen, Heiligman, & Lo (1984).
The maser emission consists of a bright core
with several distinct components near the systemic velocity arranged
in an elongated region
(Greenhill et al. 1995),
as well as "satellite" lines separated by
± 800 - 1000 km s-1 from the systemic features
(Nakai, Inoue, & Miyoshi 1993).
The presence of high-velocity emission was suggestive of a disk rotating
about a central mass of ~ 107
M
= 1.35 cm from the
nucleus of the low-luminosity Seyfert 2 galaxy NGC 4258 was detected by
Claussen, Heiligman, & Lo (1984).
The maser emission consists of a bright core
with several distinct components near the systemic velocity arranged
in an elongated region
(Greenhill et al. 1995),
as well as "satellite" lines separated by
± 800 - 1000 km s-1 from the systemic features
(Nakai, Inoue, & Miyoshi 1993).
The presence of high-velocity emission was suggestive of a disk rotating
about a central mass of ~ 107
M (Watson & Wallin 1994),
and the breakthrough observation came when
Miyoshi et al. (1995)
used the Very
Long Baseline Array to map out the positions of the high-velocity
features. They found that the satellite masers traced out a
near-perfect Keplerian velocity curve on either side of the nucleus,
allowing a precise determination of the enclosed mass within the inner
radius of the disk (3.9 milliarcsec, corresponding to a radius of only
0.14 pc). For a distance of 7.2 Mpc, the central mass is found to be
3.9 × 107
M
(Watson & Wallin 1994),
and the breakthrough observation came when
Miyoshi et al. (1995)
used the Very
Long Baseline Array to map out the positions of the high-velocity
features. They found that the satellite masers traced out a
near-perfect Keplerian velocity curve on either side of the nucleus,
allowing a precise determination of the enclosed mass within the inner
radius of the disk (3.9 milliarcsec, corresponding to a radius of only
0.14 pc). For a distance of 7.2 Mpc, the central mass is found to be
3.9 × 107
M . It
is very unlikely that this mass could be
composed of a cluster of dark objects such as stellar remnants or
brown dwarfs, since the cluster density would be so large that its
lifetime against evaporation or collisions would be short compared to
the age of the galaxy
(Maoz 1995,
1998).
This makes NGC 4258 the most
compelling dynamical case for the existence of a supermassive black
hole outside of our own Galaxy. Recently, a preliminary analysis of
HST stellar-dynamical data for NGC 4258 has yielded a value of
MBH consistent with the maser measurement
(Siopis et al. 2002);
this is a reassuring confirmation of the stellar-dynamical technique.
. It
is very unlikely that this mass could be
composed of a cluster of dark objects such as stellar remnants or
brown dwarfs, since the cluster density would be so large that its
lifetime against evaporation or collisions would be short compared to
the age of the galaxy
(Maoz 1995,
1998).
This makes NGC 4258 the most
compelling dynamical case for the existence of a supermassive black
hole outside of our own Galaxy. Recently, a preliminary analysis of
HST stellar-dynamical data for NGC 4258 has yielded a value of
MBH consistent with the maser measurement
(Siopis et al. 2002);
this is a reassuring confirmation of the stellar-dynamical technique.
 (Greenhill et al. 1996).
NGC 4945 contains high-velocity maser clumps in a
roughly disklike arrangement, but with larger uncertainties than for NGC 4258;
the central mass is ~ 106
M
(Greenhill et al. 1996).
NGC 4945 contains high-velocity maser clumps in a
roughly disklike arrangement, but with larger uncertainties than for NGC 4258;
the central mass is ~ 106
M within a radius of 0.3 pc
(Greenhill et al. 1997).
Recently, high-velocity maser features have been detected in IC 2560
(Ishihara et al. 2001),
NGC 5793
(Hagiwara et al. 2001),
NGC 2960
(Henkel et al. 2002),
and the Circinus galaxy
(Greenhill et al. 2003),
and VLBI measurements can determine whether
the masers in these galaxies trace out Keplerian rotation curves.
Additional maser disks will continue to be found in future surveys,
although the nearby AGN population has now been surveyed so thoroughly
that it is unlikely that many more new examples will be found at
distances comparable to that of NGC 4258.
within a radius of 0.3 pc
(Greenhill et al. 1997).
Recently, high-velocity maser features have been detected in IC 2560
(Ishihara et al. 2001),
NGC 5793
(Hagiwara et al. 2001),
NGC 2960
(Henkel et al. 2002),
and the Circinus galaxy
(Greenhill et al. 2003),
and VLBI measurements can determine whether
the masers in these galaxies trace out Keplerian rotation curves.
Additional maser disks will continue to be found in future surveys,
although the nearby AGN population has now been surveyed so thoroughly
that it is unlikely that many more new examples will be found at
distances comparable to that of NGC 4258.
 and
C III]
and
C III]
 1909 have longer
lag times as well as narrower widths. Thus, if lag times
tlag can be measured for
multiple broad emission lines in a given galaxy, it is possible to
trace out the velocity structure of the BLR as a function of radius.
Peterson & Wandel (1999,
2000)
and Onken & Peterson (2002)
have shown that for four of the best-observed reverberation targets,
NGC 3783, NGC 5548, NGC 7469, and 3C 390.3, the relation between
tlag and emission-line width shows exactly the
dependence expected for
Keplerian motion. Within the measurement uncertainties, the emission
lines in each galaxy yield a correlation consistent with FWHM
1909 have longer
lag times as well as narrower widths. Thus, if lag times
tlag can be measured for
multiple broad emission lines in a given galaxy, it is possible to
trace out the velocity structure of the BLR as a function of radius.
Peterson & Wandel (1999,
2000)
and Onken & Peterson (2002)
have shown that for four of the best-observed reverberation targets,
NGC 3783, NGC 5548, NGC 7469, and 3C 390.3, the relation between
tlag and emission-line width shows exactly the
dependence expected for
Keplerian motion. Within the measurement uncertainties, the emission
lines in each galaxy yield a correlation consistent with FWHM
 tlag0.5,
and for each galaxy the time lags and linewidths of the different
emission lines give consistent results for the central mass.
tlag0.5,
and for each galaxy the time lags and linewidths of the different
emission lines give consistent results for the central mass.
 *
relation of inactive galaxies.
Nelson (2000)
performed a similar analysis for a larger sample, using [O III]
linewidths as a substitute for
*
relation of inactive galaxies.
Nelson (2000)
performed a similar analysis for a larger sample, using [O III]
linewidths as a substitute for
 *,
and found similar results albeit with
additional scatter that could be attributed to some non-gravitational
motion in the narrow-line region. Some previous studies had found the
puzzling result that the AGNs seemed to have systematically lower
MBH / Mbulge ratios than inactive
galaxies
(Ho 1999,
Wandel 1999).
Since the AGNs do not appear discrepant in the
MBH -
*,
and found similar results albeit with
additional scatter that could be attributed to some non-gravitational
motion in the narrow-line region. Some previous studies had found the
puzzling result that the AGNs seemed to have systematically lower
MBH / Mbulge ratios than inactive
galaxies
(Ho 1999,
Wandel 1999).
Since the AGNs do not appear discrepant in the
MBH -
 *
relation, a likely conclusion is that the bulge luminosities of the
Seyferts had been systematically overestimated, due to a combination of
their relatively large distances and the dominance of the central point
sources; possible starburst activity in the Seyferts could further
bias the photometric decompositions toward anomalously high bulge
luminosities.
*
relation, a likely conclusion is that the bulge luminosities of the
Seyferts had been systematically overestimated, due to a combination of
their relatively large distances and the dominance of the central point
sources; possible starburst activity in the Seyferts could further
bias the photometric decompositions toward anomalously high bulge
luminosities.
 *
relation of Seyferts with
that of inactive galaxies suggests that the reverberation masses are
probably accurate to a factor of ~ 3 on average
(Peterson 2003).
Direct measurements of MBH in reverberation-mapped
Seyferts with
HST would be a valuable cross-check, but unfortunately only a few
bright Seyfert 1 galaxies are near enough for
rG to be resolved, and
attempts to perform stellar-dynamical measurements of the nearest
objects with HST have been thwarted by the dominance of the bright
nonstellar continuum. Gas-dynamical observations are not affected by
this problem, but HST spectra have found disturbed kinematics in the
narrow-line region, rendering gas-dynamical studies difficult or
impossible. While there have been attempts to detect cleanly rotating
gas that could be used for dynamical measurements
(Winge et al. 1999),
the presence of outflows typically prevents the use of spatially
resolved emission lines as a probe of MBH (e.g.,
Crenshaw et al. 2000).
Since there is no way to perform direct stellar- or
gas-dynamical measurements of
MBH in most reverberation-mapped AGNs,
the comparison with the MBH -
*
relation of Seyferts with
that of inactive galaxies suggests that the reverberation masses are
probably accurate to a factor of ~ 3 on average
(Peterson 2003).
Direct measurements of MBH in reverberation-mapped
Seyferts with
HST would be a valuable cross-check, but unfortunately only a few
bright Seyfert 1 galaxies are near enough for
rG to be resolved, and
attempts to perform stellar-dynamical measurements of the nearest
objects with HST have been thwarted by the dominance of the bright
nonstellar continuum. Gas-dynamical observations are not affected by
this problem, but HST spectra have found disturbed kinematics in the
narrow-line region, rendering gas-dynamical studies difficult or
impossible. While there have been attempts to detect cleanly rotating
gas that could be used for dynamical measurements
(Winge et al. 1999),
the presence of outflows typically prevents the use of spatially
resolved emission lines as a probe of MBH (e.g.,
Crenshaw et al. 2000).
Since there is no way to perform direct stellar- or
gas-dynamical measurements of
MBH in most reverberation-mapped AGNs,
the comparison with the MBH -
 *
relation remains the main consistency
check that can currently be applied to the reverberation-based masses.
*
relation remains the main consistency
check that can currently be applied to the reverberation-based masses.
 L0.7.
This correlation offers an extremely valuable shortcut to
estimate the BLR size, and black hole mass, in distant quasars. While
reverberation campaigns require years of intensive observations,
L(5100 Å) and
FWHM(H
L0.7.
This correlation offers an extremely valuable shortcut to
estimate the BLR size, and black hole mass, in distant quasars. While
reverberation campaigns require years of intensive observations,
L(5100 Å) and
FWHM(H )
can be measured from a single spectrum,
and then combined to yield an estimate of
MBH under the assumption
of virial motion of the BLR clouds. This is the only technique that
can routinely be applied to derive
MBH in distant AGNs, and it has
recently been the subject of intense interest, with numerous studies
focused on topics such as the MBH /
Mbulge ratio in quasars and the
search for possible differences between radio-loud and radio-quiet
objects (e.g.,
Laor 1998;
McLure & Dunlop 2001;
Lacy et al. 2001;
Laor 2001;
Oshlack, Webster, & Whiting 2002;
McLure & Dunlop 2002;
Jarvis & McLure 2002;
Shields et al. 2002).
The technique has also
been extended to make use of continuum luminosity in the rest-frame
ultraviolet combined with the velocity width of either C IV
(Vestergaard 2002)
or Mg II
(McLure & Jarvis 2002),
so that ground-based, optical spectra can be used to derive black hole
masses for high-redshift quasars.
)
can be measured from a single spectrum,
and then combined to yield an estimate of
MBH under the assumption
of virial motion of the BLR clouds. This is the only technique that
can routinely be applied to derive
MBH in distant AGNs, and it has
recently been the subject of intense interest, with numerous studies
focused on topics such as the MBH /
Mbulge ratio in quasars and the
search for possible differences between radio-loud and radio-quiet
objects (e.g.,
Laor 1998;
McLure & Dunlop 2001;
Lacy et al. 2001;
Laor 2001;
Oshlack, Webster, & Whiting 2002;
McLure & Dunlop 2002;
Jarvis & McLure 2002;
Shields et al. 2002).
The technique has also
been extended to make use of continuum luminosity in the rest-frame
ultraviolet combined with the velocity width of either C IV
(Vestergaard 2002)
or Mg II
(McLure & Jarvis 2002),
so that ground-based, optical spectra can be used to derive black hole
masses for high-redshift quasars.
 5 × 108
M
5 × 108
M )
and in luminosity (
)
and in luminosity ( L
L
 7 × 1045 erg s-1 at 5100
Å). Application of this method to high-redshift, high-luminosity
quasars necessarily involves a large extrapolation (see
Netzer 2003
for further discussion). These issues can be overcome if
reverberation masses can be derived for larger samples of quasars,
extending to high intrinsic luminosities and
MBH > 109
M
7 × 1045 erg s-1 at 5100
Å). Application of this method to high-redshift, high-luminosity
quasars necessarily involves a large extrapolation (see
Netzer 2003
for further discussion). These issues can be overcome if
reverberation masses can be derived for larger samples of quasars,
extending to high intrinsic luminosities and
MBH > 109
M , so
that the relations between MBH, linewidth, and
luminosity can be calibrated over a broader parameter space.
, so
that the relations between MBH, linewidth, and
luminosity can be calibrated over a broader parameter space.
1.5. Future Work and Some Open Questions
 *
and MBH-Lbul correlations can be
determined definitively. To
constrain the amount of intrinsic scatter in these correlations,
realistic estimates of the measurement uncertainties are crucial.
Gas-dynamical measurements with HST and, in the future, from
ground-based telescopes with adaptive optics, will be a key
component of this pursuit. Additional measurements of black hole
masses from maser dynamics will be extremely valuable as well, if
more galaxies with Keplerian maser disks can be found.
*
and MBH-Lbul correlations can be
determined definitively. To
constrain the amount of intrinsic scatter in these correlations,
realistic estimates of the measurement uncertainties are crucial.
Gas-dynamical measurements with HST and, in the future, from
ground-based telescopes with adaptive optics, will be a key
component of this pursuit. Additional measurements of black hole
masses from maser dynamics will be extremely valuable as well, if
more galaxies with Keplerian maser disks can be found.
 *.
*.
 gas /
vrot
gas /
vrot
 1?
Again, direct comparisons with stellar-dynamical
observations would be very useful.
1?
Again, direct comparisons with stellar-dynamical
observations would be very useful.
 for
some objects (e.g.,
Shields et al. 2002),
but these measurements involve extrapolating the known correlation between
rBLR and L far beyond the mass and
luminosity ranges over which it has been calibrated locally. At
the other extreme, is there a lower limit to
Lbul or
for
some objects (e.g.,
Shields et al. 2002),
but these measurements involve extrapolating the known correlation between
rBLR and L far beyond the mass and
luminosity ranges over which it has been calibrated locally. At
the other extreme, is there a lower limit to
Lbul or
 *
below which galaxies have no central black hole at all?
Searches for nuclear activity in dwarf galaxies can offer some
constraints on the population of black holes with M <
106
M
*
below which galaxies have no central black hole at all?
Searches for nuclear activity in dwarf galaxies can offer some
constraints on the population of black holes with M <
106
M .
The case of NGC 4395, a dwarf Magellanic spiral hosting a
full-fledged Seyfert 1 nucleus
(Filippenko & Sargent 1989),
demonstrates that at least some dwarf galaxies can host black holes
that would be undetectable by dynamical means.
.
The case of NGC 4395, a dwarf Magellanic spiral hosting a
full-fledged Seyfert 1 nucleus
(Filippenko & Sargent 1989),
demonstrates that at least some dwarf galaxies can host black holes
that would be undetectable by dynamical means.
 *
and MBH - Lbul correlations evolve with
redshift, and how early did the black holes in the highest-redshift
quasars build up most of their mass? Reverberation mapping of
high-redshift quasars, and further calibration and testing of the
rBLR-luminosity relationship in luminous quasars, will
be of fundamental importance in answering these questions. Measurement
of the masses of black holes at high redshift, as well as the
luminosities and/or velocity dispersions of their host galaxies,
will be a major observational step toward understanding the
coevolution of black holes and their host galaxies.
*
and MBH - Lbul correlations evolve with
redshift, and how early did the black holes in the highest-redshift
quasars build up most of their mass? Reverberation mapping of
high-redshift quasars, and further calibration and testing of the
rBLR-luminosity relationship in luminous quasars, will
be of fundamental importance in answering these questions. Measurement
of the masses of black holes at high redshift, as well as the
luminosities and/or velocity dispersions of their host galaxies,
will be a major observational step toward understanding the
coevolution of black holes and their host galaxies.
Bibliography
Antonucci, R. R. J., & Miller, J. S.
1985, ApJ, 297, 621
Baker, J. C., & Hunstead, R. W.
1995, ApJ, 452, L95
Barth, A. J., Sarzi, M., Rix, H.-W., Ho, L. C.,
Filippenko, A. V., & Sargent, W. L. W.
2001, ApJ, 555, 685
Binney, J., & Tremaine, S.
1987, Galactic Dynamics (Princeton: Princeton
University Press)
Blandford, R. D., & McKee, C. F.
1982, ApJ, 255, 419
Böker, T., Laine, S., van der Marel, R. P.,
Sarzi, M., Rix, H.-W., Ho, L. C., & Shields, J. C.
2002, AJ, 123, 1389
Bower, G. A., et al.
1998, ApJ, 492, L111
Braatz, J. A., Wilson, A. S., & Henkel, C.
1996, ApJS, 106, 51
Braatz, J. A., Wilson, A. S., & Henkel, C.
1997, ApJS, 110, 321
Cappellari, M., Verolme, E. K., van der Marel,
R. P., Verdoes Kleijn, G. A., Illingworth, G. D., Franx, M., Carollo, C. M.,
& de Zeeuw, P. T. 2002, ApJ, in press
Carollo, C. M., Stiavelli, M., & Mack, J.
1998, AJ, 116, 68
Chokshi, A., & Turner, E. L.
1992, MNRAS, 259, 421
Claussen, M. J., Heiligman, G. M., & Lo, K. Y.
1984, Nature, 310, 298
Crenshaw, D. M., et al.
2000, AJ, 120, 1731
Cretton, N., Rix, H.-W., & de Zeeuw, P. T.
2000, ApJ, 536, 319
de Koff, S., Best, P., Baum, S. A., Sparks, W.,
Röttgering, H., Miley, G., Golombek, D., Macchetto, F., &
Martel, A.
2000, ApJS, 129, 33
Ferrarese, L., Ford, H. C., & Jaffe, W.
1996, ApJ, 470, 444
Ferrarese, L., & Ford, H. C.
1999, ApJ, 515, 583
Ferrarese, L. & Merritt, D.
2000, ApJ, 539, L9
Ferrarese, L., Pogge, R. W., Peterson, B. M.,
Merritt, D., Wandel, A., & Joseph, C. L.
2001, ApJ, 555, L79
Fillmore, J. A., Boroson, T. A., & Dressler, A.
1986, ApJ, 302, 208
Filippenko, A. V., & Sargent, W. L. W.
1989, ApJ, 342, L11
Ford, H. C., et al.
1994, ApJ, 435, L27
Gebhardt, K., et al.
2000a, ApJ, 539, L13
Gebhardt, K., et al.
2000b, ApJ, 543, L5
Greenhill, L. J., Jiang, D. R., Moran, J. M., Reid,
M. J., Lo, K. Y., & Claussen, M. J.
1995, ApJ, 440, 619
Greenhill, L. J., Gwinn, C. R., Antonucci, R., &
Barvainis, R.
1996, ApJ, 472, L21
Greenhill, L. J., Moran, J. M., & Herrnstein,
J. R.
1997, ApJ, 481, L23
Greenhill, L. J., et al.
2002, ApJ, 565, 836
Greenhill, L. J., Kondratko, P. T., Lovell,
J. E. J., Kuiper, T. B. H., Moran, J. M., Jauncey, D. L., & Baines,
G. P. 2003, ApJ, in press
Hagiwara, Y., Diamond, P. J., Nakai, N., &
Kawabe, R.
2001, ApJ, 560, 119
Harms, R. J., et al.
1994, ApJ, 435, L35
Henkel, C., Braatz, J. A., Greenhill, L. J., &
Wilson, A. S.
2002, A&A, 394, L23
Ho, L.C. 1999, in
Observational Evidence for Black Holes in the Universe,
ed. S.K. Chakrabarti (Dordrecht: Kluwer), 157
Ho, L.C., Sarzi, M., Rix, H., Shields, J.C.,
Rudnick, G., Filippenko, A.V., & Barth, A.J.
2002, PASP, 114, 137
Ishihara, Y., Nakai, N., Iyomoto, N., Makishima, K.,
Diamond, P., & Hall, P.
2001, PASJ, 53, 215
Iwasawa, K., et al.
1996, MNRAS, 282, 1038
Iwasawa, K., Maloney, P. R., & Fabian, A. C.
2002, MNRAS, 336, L71
Jaffe, W., Ford, H. C., Ferrarese, L., van den
Bosch, F., & O'Connell, R. W.
1993, Nature, 364, 213
Jaffe, W., Ford, H. C., Tsvetanov, Z.,
Ferrarese, L., & Dressel, L. 1999, in
ASP Conf. Series Vol. 182, Galaxy Dynamics, edited by
D. Merritt, J. A. Sellwood, & M. Valluri (San Francisco: ASP), 13
Jarvis, M. J., & McLure, R. J.
2002, MNRAS, 336, L38
Kaspi, S., Smith, P. S., Netzer, H., Maoz, D.,
Jannuzi, B. T., & Giveon, U.
2000, ApJ, 533, 631
Kaspi, S., Netzer, H., Maoz, D., Shemmer, O.,
Brandt, W. N., & Schneider, D. P. 2003, in
Active Galactic Nuclei: from Central Engine
to Host Galaxy, edited by S. Collin et al. (San Francisco: ASP)
Koda, J., & Wada, K.
2002, A&A, 396, 867
Kormendy, J., & Gebhardt, K. 2001, in
The 20th Texas Symposium on Relativistic
Astrophysics, ed. J. Craig Wheeler & Hugo Martel (New York:
AIP), 363
Kormendy, J., & Richstone, D.
1995, ARA&A, 33, 581
Kormendy, J., & Westpfahl, D. J.
1989, ApJ, 338, 752
Kotanyi, C. G., & Ekers, R. D.
1979, A&A, 73, L1
Krolik, J. H.
2001, ApJ, 551, 72
Lacy, M., Laurent-Muehleisen, S. A., Ridgway, S. E.,
Becker, R. H., & White, R. L.
2001, ApJ, 551, L17
Laor, A.
1998, ApJ, 505, L83
Laor, A.
2001, ApJ, 553, 677
Macchetto, F., Marconi, A., Axon, D. J.,
Capetti, A., Sparks, W., & Crane, P.
1997, ApJ, 489, 579
Maciejewski, W. 2003, in
Carnegie Observatories Astrophysics Series, Vol. 1: Coevolution of Black
Holes and Galaxies, ed. L. C. Ho (Pasadena: Carnegie Observatories,
http://www.ociw.edu/ociw/symposia/series/symposium1/proceedings.html)
Maciejewski, W., & Binney, J.
2001, MNRAS, 323, 831
Makishima, K., et al.
1994, PASJ, 46, L77
Maoz, E.
1995, ApJ, 447, L91
Maoz, E.
1998, ApJ, 494, L181
Marconi, A., Capetti, A., Axon, D. J.,
Koekemoer, A., Macchetto, D., & Schreier, E. J.
2001, ApJ, 549, 915
Marconi, A., et al.
2003, ApJ, in press
McLure, R. J., & Dunlop, J. S.
2001, MNRAS, 327, 199
McLure, R. J., & Dunlop, J. S.
2002, MNRAS, 331, 795
McLure, R. J., & Jarvis, M. J.
2002, MNRAS, in press
Merritt, D., & Ferrarese, L. 2001, in
The Central Kiloparsec of Starbursts and AGNs,
ed. J. H. Knapen et al. (San Francisco: ASP), 335
Miyoshi, M., Moran, J., Herrnstein, J., Greenhill,
L., Nakai, N., Diamond, P., & Inoue, M.
1995, Nature, 373, 127
Moran, J. M., Greenhill, L. J., &
Herrnstein, J. R.
1999, Journal of Astrophysics and Astronomy, 20, 165
Nakai, N., Inoue, M., & Miyoshi, M.
1993, Nature, 361, 6407
Nandra, K., George, I. M., Mushotzky, R. F., Turner,
T. J., & Yaqoob, T.
1997, ApJ, 477, 602
Nelson, C. H.
2000, ApJ, 544, L91, 199
Netzer, H.
2003, ApJ, 583, L5
Onken, C. A., & Peterson, B. M.
2002, ApJ, 572, 746
Oshlack, A. Y. K. N., Webster, R. L., & Whiting,
M. T.
2002, ApJ, 576, 81
Peterson, B. M. 2001, in
Advanced Lectures on the Starburst-AGN Connection,
ed. I. Aretxaga, D. Kunth, & R. Mújica (Singapore: World
Scientific), 3
Peterson, B. M. 2003, in
Active Galactic Nuclei: from Central Engine
to Host Galaxy, edited by S. Collin et al. (San Francisco: ASP)
Peterson, B. M., & Wandel, A.
1999, ApJ, 521, L95
Peterson, B. M., & Wandel, A.
2000, ApJ, 540, L13
Rees, M. J.
1984, ARA&A, 22, 471
Sadler, E. M., & Gerhard, O. E.
1985, MNRAS, 214, 177
Salucci, P., Ratnam, C., Monaco, P., &
Danese, L.
2000, MNRAS, 317, 488
Salpeter, E. E.
1964, ApJ, 140, 796
Sargent, W. L. W., Young, P. J., Boksenberg, A.,
Shortridge, K., Lynds, C. R., & Hartwick, F. D. A.
1978, ApJ, 221, 731
Sarzi, M., Rix, H.-W., Shields, J. C., Rudnick, G.,
Ho, L. C., McIntosh, D. H., Filippenko, A. V., & Sargent, W. L. W.
2001, ApJ, 550, 65
Sarzi, M. et al.
2002, ApJ, 567, 237
Shields, G. A., Gebhardt, K., Salviander, S., Wills,
B., Xie, B., Brotherton, M. S., Yuan, J., Dietrich, M.
2002, ApJ, 583, 124
Siopis, C., et al.
2002, BAAS, 201, 6802
Small, T. A., & Blandford, R. D.
1992, MNRAS, 259, 725
Soltan, A.
1982, MNRAS, 200, 115
Tanaka, Y., et al.
1995, Nature, 375, 659
Tran, H. D., Tsvetanov, Z., Ford, H. C., Davies, J.,
Jaffe, W., van den Bosch, F. C., & Rest, A.
2001, AJ, 121, 2928
Tremaine, S., et al.
2002, ApJ, 574, 740
van der Marel, R. P.
1994, ApJ, 432, L91
Verdoes Kleijn, G. A., Baum, S. A., de Zeeuw, P. T.,
& O'Dea, C. P.
1999, AJ, 118, 2592
Verdoes Kleijn, G. A., van der Marel, R. P.,
Carollo, C. M., & de Zeeuw, P. T.
2000, AJ, 120, 1221
Verdoes Kleijn, G. A., van der Marel, R. P., de
Zeeuw, P. T., Noel-Storr, J., & Baum, S. A.
2002, AJ, in press
Verdoes Kleijn, G. A., van der Marel, R. P., &
Noel-Storr, J. 2003, in
Carnegie Observatories Astrophysics Series, Vol. 1:
Coevolution of Black Holes and Galaxies, ed. L. C. Ho (Pasadena:
Carnegie Observatories,
http://www.ociw.edu/ociw/symposia/series/symposium1/proceedings.html)
Vestergaard, M.
2002, ApJ, 571, 733
van der Marel, R. P., & van den Bosch, F. C.
1998, AJ, 116, 2220
Wada, K., Meurer, G., & Norman, C. A.
2002, ApJ, 577, 197
Walcher, C. J., Häring, N., Böker, T.,
Rix, H.-W., van der Marel, R. P., & Gerssen, J. 2003, in
Carnegie Observatories Astrophysics Series, Vol. 1: Coevolution of Black
Holes and Galaxies, ed. L. C. Ho (Pasadena: Carnegie Observatories,
http://www.ociw.edu/ociw/symposia/series/symposium1/proceedings.html)
Wandel, A.
1999, ApJ, 519, L39
Wandel, A., Peterson, B. M., & Malkan, M. A.
1999, ApJ, 526, 579
Watson, W. D. & Wallin, B. K.
1994, ApJ, 432, L35
Whiting, M. T., Webster, R. L., & Francis,
P. J.
2001, MNRAS, 323, 718
Wilkes, B. J., Schmidt, G. D., Smith, P. S.,
Mathur, S., & McLeod, K. K.
1995, ApJ, 455, L13
Winge, C., Axon, D. J., Macchetto, F. D., Capetti,
A., & Marconi, A.
1999, ApJ, 519, 134
Young, P. J., Westphal, J. A., Kristian, J.,
Wilson, C. P., & Landauer, F. P.
1978, ApJ, 221, 721
Zel'dovich, Ya. B., & Novikov, I. D.
1964, Sov. Phys. Dokl., 158, 811