Copyright © 1997 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 1997. 35:
101-136 Copyright © 1997 by Annual Reviews. All rights reserved |
de Vaucouleurs (1983)
differentiated between what he called the Malmquist effect (the progressive
truncation of the luminosity function at increasing distances in a
magnitude-limited
sample) and the Malmquist bias in the distances derived from such a sample.
One may intuitively think that if there is a way of classifying galaxies
into absolute magnitude bins, for example, by using de Vaucouleurs's
luminosity
index or the TF relation M = ap + b, the Malmquist effect,
as defined above, will certainly cut away fainter galaxies from the
sample, but then the parameter p
"glides" simultaneously. de Vaucouleurs argues that this compensates for
the systematic distance dependent effect. However, the theory of the
Malmquist bias of the second kind in direct TF distance modulus shows
that such a compensation
is not complete: Average p glides to larger values, but still, no
matter what the value of p is, the corresponding distribution of
true M is cut at a common Mlim
that depends only on the distance. One cannot escape this fact, which means
that in the observed sample, the distance indicator relation <M> =
ap + b is necessarily distorted and causes the second kind
of Malmquist bias. However, at each distance the bias is smaller by the
factor 
2 /
(2 +
M2),
as compared with the simple truncation effect of the luminosity function
with dispersion
M.
5.1. The Ideal Case of the Inverse Relation
In the ideal case, the TF parameter p is not restricted by any such observational limit as Mlim. Hence, at any distance, the distribution of observed p corresponding to a fixed M, and especially its average <p>M, is the same. Schechter (1980) thus realized that the inverse relation
 |
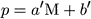(13) |
has the useful property that it may be derived in an unbiased manner from magnitude-limited samples, if there is no selection according to p. He used this relation in a study of the local extragalactic velocity field, which requires that kinematic distances minimize the p residuals (see also Aaronson et al 1982).
In what manner could one use the inverse relation as a concrete distance indicator? Assume that there is a cluster of galaxies at true distance modulus µ. Derive the distance modulus for each galaxy i that has pi measured, using the inverse relation as a "predictor" of M: µi = m -(1/a')(p - b'). Teerikorpi (1984) showed that the distance estimate <µi> is unbiased, under the condition that there is no observational restriction to p. This result was supported by numerical simulations in Tully (1988).
Our ordinary way of thinking about distance indicators is closely linked to the direct relation: Measure p, determine from the relation what is the expected <M>, and calculate µ = m - <M> for this one object. The use of the inverse relation is at first intuitively repugnant because one tends to look at the predictor of M, (1/a')(p - b'), similarly as one looks at the direct relation. The direct distance moduli are "individuals," whereas the inverse relation is a kind of collective distance indicator: Measure the average p for the sample and calculate from <m> and <p> the distance modulus. Restriction to one galaxy, which is so natural with the direct relation, means restricting the value of p to the one observed, which is not allowed with the inverse relation.
From a m - p diagram (Figure 3) showing a "calibrator" (nearby) cluster and a more distant cluster, one can easily explain the secret of the inverse relation. Let us put the calibrator sample at 10 pc, so that m = M. The cluster to be measured is at the unknown distance modulus µ and is cut by the magnitude limit mlim. Glide the calibrator cluster along the m axis by the amount of µ. Then the inverse regression lines are superimposed. This means that the observed average of p at m is <p>m for the second cluster, which is the same as for the calibrator cluster at M = m - µ. From this, it follows that <µ>m = m - (<p>m - b') / a' and, by averaging over all m, that
 |
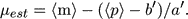(14) |
The (p, M) data form a scattered bivariate distribution, and without further knowledge of the reason for the scatter, one has the freedom, within the limits of what is the application and what is known about the selection of p and M parameters, to use either the direct or the inverse relation. Even if the scatter is not due to errors in p or natural processes that shift p at constant M, Figure 3 shows that one may use the inverse relation if the bivariate distributions of the calibrator and distant samples are the same. On the other hand, even if there is error in p, one may choose to use the direct relation if the application requires it (Bottinelli et al 1986, Lynden-Bell et al 1988). Naturally, another problem and source of biases is that the bivariate distribution may not fulfill the conditions of gaussianity, which are required in the derivation of the regression lines (Bicknell 1992, Ekholm & Teerikorpi 1997), or the calibrator and distant samples have, for example, different measurement accuracy in magnitude (Teerikorpi 1990, Fouqué et al 1990).
Finally, the inverse relation does not require that its calibrators form a volume-limited sample, which is necessary for the correct calibration of the direct relation. This is also illustrated by Figure 3 because the regression line of the calibrator sample is not changed if a portion m > some mlim is cut away from it.