1.2. Polarimetry

The large majority of recent observations of medium-scale and large-scale magnetic fields were in radio astronomy (e.g., cm, mm, submm/extreme-infrared wavelengths), with some additional observations from optical astronomy (e.g., µm wavelengths).

The methods employed to study the magnetic fields in Milky Way objects are similar to the ones used to study the magnetic fields in other galaxies. The methods of Faraday rotation, synchrotron equipartition, and cosmic-ray collisions as discussed at length in Section 4.1, while the methods of dust grain emission and absorption and of Zeeman splitting are discussed more fully in Section 2.1. The two main methods largely used (Faraday rotation, grain emission) are briefly outlined below.

Rotatable polarimeters give the position angle of the electric vector at maximum intensity for the incoming radiation, as well as the percentage of the incoming radiation that is linearly polarized. Observing wise, for detecting a source that is 4% linearly polarized, one requires more time by a factor 1 / (0.04)² = 625 at the telescope for detecting the polarized signal than for detecting the total continuum emission.

One important physical phenomenon used to measure medium-scale magnetic fields is thermal dust emission. Thermal dust emission processes from dust particles aligned by the magnetic fields in interstellar clouds show linearly polarized continuum emission in the extreme infrared (mm and submm wavelengths) and far infrared (e.g., 100 µm), allowing the study and the mapping of the magnetic fields in large clouds. In emission, the position angle PA of the electric vector at maximum intensity is perpendicular to the magnetic field lines. To study magnetic fields at moderate thermal density, it is best to use telescope at submm wavelengths, because of the following. At cm and long mm wavelengths, there is often not enough signal from dust in many cases (poor signal to noise ratio). At far infrared wavelengths, there are costly airborne flights necessary. At near infrared and optical wavelengths one has to cope with several physical problems: (i) multiple scatterings that induce polarization, independent of magnetic fields, (ii) the need to find bright background sources behind clouds, (iii) the ambiguity between one magnetic field direction and its opposite, and (iv) there is no secure method to get the magnetic field strength. Scarrott (1996) reviews the limited data obtained by optical observations, while Scarrott et al. (1996) argue for a mixture of two mechanisms to explain optical polarization data in the galaxy NGC 5128.

One important physical phenomenon used to deduce the large-scale galactic magnetic field is the Faraday rotation effect. Large scale magnetic fields in spiral galaxies are studied primarily through Faraday rotation of nearby pulsars and of distant galaxies and quasars. Due to the well known Faraday rotation observable at centimeter wavelengths, the change of the position angle PA of the electric vector at maximum intensity PA with wavelength , follows the Faraday formula: PA = (RM) ^{. 2} , where PA is in radians, is in m, and RM is the rotation measure (rad./m²). One has: RM = 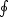0.8n_e ^. B_I ^. dL where n_e is the free electron density (cm^-3), B_I is the magnetic field (µgauss) component parallel to the line of sight, and L is the length (pc) along the line of sight. The RM is the linear sum of the individual contributions from the radio emitter (a galaxy or a quasar, say), from the intracluster medium around the source, the intergalactic medium between clusters of galaxies (quite negligible), and from the interstellar medium in our Galaxy (in spiral arms and in large interstellar bubbles). A catalogue of unambiguous rotation measure for 674 galaxies and quasars was published by Broten et al. (1988). It contains sources whose data had been selected in one physical wavelength range only, to cover a single physical régime, that of a Faraday-thin, one-component, spectrum-limited source.

Galactic magnetic fields can be split into a random component B_ran and a uniform (ie regular) component B_reg, and these components can be added in the usual quadratic way: B_tot² = B_reg² + B_ran². The random component is on average twice as strong as the uniform component (B_reg 0.5B_ran, e.g., Table 2 in Vallée 1984a). In the Milky Way, the uniform component was found to be oriented nearly azimuthally, i.e., locally towards galactic longitude l 90° (e.g., equation 5 in Vallée 1983a).

Important subtleties involved in deducing polarization and in interpreting them, to alert the theoretical reader to the pitfalls in interpreting the data, can be found in Sections 3 and 4 here, as well as elsewhere (e.g., Vallée 1980; Heiles 1987; Kronberg 1994; Vallée 1995a; Vallée 1996a; Vallée 1996b).

The aim of the present review is to highlight the salient discoveries, on the subject of magnetic fields on mid scales and large scales. Section 2 deals with medium and large objects within our Milky Way, while Section 3 deals with the Milky Way as a whole. Sections 4 and 5 study the nearby galaxies and the more distant objects.