2.3. Interstellar Superbubbles and shells with B ~ n¹ (~ 50 to 500 pc)

Figure 4 shows the sky distribution of the 662 quasars (QSO) and galaxies with a measured Faraday Rotation Measure RM, done with the help of a Mercator projection of the galactic coordinates. Data from Broten et al. (1988). From such catalogues, one deduces the distribution (direction, strength) of the magnetic fields.

Figure 4. Sky distribution of quasars and galaxies with a known Faraday rotation measure (RM) value. A Mercator projection of galactic coordinates is used (galactic longitudes on horizontal axis; galactic latitudes on vertical axis). The Galactic Centre is at 0°, 0°. Zones of negative RM (empty circles - magnetic field going away from the Sun) alternate with zones of positive RM (filled circles - magnetic field coming toward the Sun). The two nearest and largest superbubbles are sketched (dashes), with Loop I/NPS centered near l = 330°, and Loop II/Cetus Arc centered near l = 110°.

We know that stellar winds from an association of OB stars can form a common superbubble, enclosed by a large supershell, through the combined effort of the winds from the stars at the center. Some authors have used the Zeeman effect in emission and others have used the Faraday effect to detect the magnetic field component B_I in some of these large superbubbles (e.g., Heiles 1989).

Some superbubbles are located close enough to the Sun that their large angular sizes can encompass the line of sights of many QSOs and galaxies, and their magnetic fields can be studied by the Faraday effect. Thus many authors have found the magnetic field component B2 in large superbubbles, as detected by radio RM observations of QSOs and galaxies. The magnetism of the "North Polar Spur" shell was first reported in Fig. 2 of Vallée & Kronberg (1973); the magnetism of the "Cetus Arc" shell was first reported in Fig. 3 of Simard-Normandin & Kronberg (1979); the magnetism of the "Gum Nebula" shell was first reported in Fig. 4 of Vallée and Bignell (1983); the magnetism of the 20° "Monogem Ring" shell was first reported in Fig. 3 of Vallée et al. (1984). Since then, magnetism has been found in other localized shells of superbubbles, e.g., Eridanus, G135-40-10, G062-23+13 (for a review, see Vallée, 1993d).

Averaging over four magnetized shells near the sun (North polar spur, Cetus arc, Gum nebula, and Monogem ring), it was found that a mean shell rotation measure of 90 radians/m² could be expected above the surrounding background (Table 1 in Vallée, 1984b). One could then not ignore the rotation measure contributions from these selected celestial zones in the total galactic contributions. These four interstellar shells, with a mean diameter 200 - 250 pc, are expanding at a mean speed of 23 km/s (e.g., Table 2 in Broten et al. 1985).

Broten et al. (1985) also found that the strength of the magnetic field in these shells increased with the relative shell compression, according to the empirical parabolic law: B_shell 3 µGauss + (9 µGauss).[inner shell radius/outer shell radius]² .

A more recent study (Vallée, 1993d) of nearby large interstellar magnetic bubbles (within 1 kpc of the Sun) showed an increase of the shell magnetic field with increasing shell thermal density, as a consequence of the narrowing of the shell width r, according to the law: B_shell = 3 µGauss ^.[1 - (1 - r / r_out)³]^-k where r_out is the outer radius of the whole shell. Here r = (outer shell radius - inner shell radius), and k is the exponent in the well-known magnetic field versus gas density relation B ~ n^k . Vallée (1993d) thus found for several nearby interstellar magnetic bubbles with observed B and observed n that B ~ n^k with observed k = 1.0 ± 0.1, as expected for an expanding shocked medium (narrow shell width).

Figure 5 shows a plot of the shell magnetic field as a function of the relative thickness of a shell, for several nearby interstellar magnetic bubbles. Curves for B ~ n^k are shown, with exponent values k = 0.0, 0.5, 1.0, 1.5, 2.0.

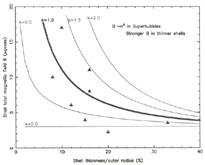Figure 5. Plot of the magnetic field strength (B, in µgauss) in large supershells as a function of the relative shell thickness (shell thickness/outer shell radius, in %), for shells with diameter > 100 pc. Continuous curves give the model behavior of the shell magnetic field with shell gas density n, of the form B ~ nk, for 0 k 2. See Vallée (1993d) for details. The observed data show a better fit to the behavior of the magnetic field given by the relation B ~ n1.0 .

The early theories of thin shells around superbubbles from combined stellar winds were adequate for explaining the primary observational features (defined as: shell age, outer shell radius, shell speed, shell mass, shell energy), but they were not adequate to explain some secondary features (defined as: shell thickness, shell magnetic field, shell gas density). More recently published theories for a stellar-wind superbubble predict a range of thick shells (e.g., Mineshige et al. 1993; Slavin and Cox 1993; Ferrière 1993a, 1993b, 1993c; Tomisaka 1992; Jun and Norman 1996; Shull 1995; Stone and Norman 1992). These later theories have been found more adequate when compared with the observations (Vallée, 1994d), showing for 9 such shells with a measured magnetic field value the presence of thick shells (mean shell thickness = 16% of outer shell radius), low shell magnetic fields (mean shell magnetic field strengths = 8µgauss), and low shell gas density (mean gas shell density = 2.4 cm^-3).

Verschuur (1993) has provided some evidence for a much bigger supershell, formed by high-velocity clouds towards l = 231° above the Perseus spiral arm, with thickness/radius of 55 pc / 1900 pc = 2.9% and a magnetic field value above 15 µGauss. If confirmed, this data point (not shown here) with such a lower B limit would not contradict the B ~ n¹ law.