3.7.1. Basic Notions

The subject of galactic dynamo theory is still in a state of flux. Here is a short description of the basics of galactic dynamos.

The basic impetus for galactic dynamos has been made by Parker (1971a); Parker (1971b), and by followers since. Dynamo theories predict a large predominance of the m_azim = 0 shape for the galactic magnetic field, but the observations show only a small predominance of that shape (due to a non-negligible number of galaxies with m_azim = 1). Why ?

Turbulent dynamo theories formulate the problem of the large-scale magnetic field in a spiral galaxy with the general equation (e.g., Parker 1971a; Parker 1971b, Ruzmaikin et al. 1985; Ruzmaikin et al. 1988; Rádler, 1995):

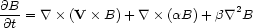where signifies a partial differential operator, t is the time, B is the global magnetic field, V is the regular velocity field (mainly due to differential rotation as a function of radius), is the mean helicity of interstellar turbulences, and is the turbulent diffusivity which represents the effect of the small scale magnetic field on the mean magnetic field.

As mentioned briefly in Section 3.5.1, the usual simple solution of this equation is achieved by separating it into 3 components in cylindrical coordinates (r, , z), and then using the WKB asymptotic method for differential equations. For B this gives a solution proportional to cos (_mazim +...), where the azimuthal angle is and the azimuthal modes m_azim = 0, 1, 2,.... For B_z this gives a dynamo-type equation with a spectrum of eigenvalues with the vertical modes p = 0, 1, 2, .... For B_r this gives a Schrödinger-type equation for the function Q(r) with the radial potential (r), where B and B_r are proportional to Q(r), and where Q(r) can be approximated by various cosine functions with the radial modes n = 0, 1, 2, ... (e.g., Fig. 5 in Ruzmaikin et al. 1985). The quasi-stationary but small number of radial reversals (n < 3) and their positions are controlled by the radial profiles of some parameters: the galactic rotation velocity, the disk thickness, and the gas density (e.g., Poezd et al. 1993).

With many galactic physical and dynamical conditions, the preferred modes are: m_azim = 0 (axisymmetric azimuthal magnetic field lines as one goes along a circle at a fixed radius) or m_azim = 1 (bisymmetric) in that order; p = 0 (same direction of magnetic field lines as one goes from below to above the galactic plane); and n = 0 (no radial reversal of the magnetic field lines as one goes from the galactic center radially outward) or n = 1 (first radial magnetic field reversal) or n = 2 (second radial magnetic field reversal) in that order. Thus for the Milky Way we have m = 0, p = 0, n = 0, 1, 2, whereas for M31 we have m = 0, p = 0, n = 0 (Poezd et al., 1993; Vallée 1991b; Vallée, 1996). There is ample evidence for an even parity across the galactic plane (p = 0) for the Milky Way, for M31, and for NGC 253 (e.g., Beck et al. 1996).